Yours but Others Use It
What belongs to you but mostly other people use it?
SOLUTION
The answer is YOUR NAME.
Unknown Author
We do not know where this puzzle originated from. If you have any information, please let us know via email.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
The Die Game
You pick a number between 1 and 6 and keep throwing a die until you get it. Does it matter which number you pick for maximizing the total sum of the numbers in the resulting sequence?
In the example below, the picked number is 6 and the total sum of the numbers in the resulting sequence is 35.
SOLUTION
No matter what number you pick, the expected value of each throw is the average of the numbers from 1 to 6 which is 3.5. The choice of the number also does not affect the odds for the number of throws until the game ends, which is 6. Therefore, the total sum is always 3.5 × 6 = 21 on average, regardless of the chosen number.
Symmetry and Perplexion
Find an X > 1, such that:
SOLUTION
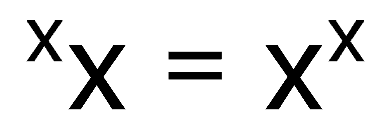
If we pick X=√2, (using a somewhat ambiguous notation) we get:
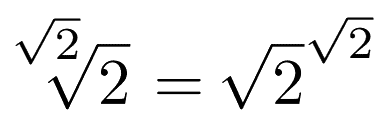
To see that the equality above holds, simply note that 2=(√2)² and take √2 root of both sides.
Peculiar Sequence of Words
What is the peculiar property of this sequence of words?
WHAT, HOLE, ALES, TEST
SOLUTION
If you take the first letter from each word, you will spell the first word in the sequence.
If you take the second letter from each word, you will spell the second word in the sequence.
If you take the third letter from each word, you will spell the third word in the sequence.
If you take the fourth letter from each word, you will spell the fourth word in the sequence.
| W | H | A | T |
| H | O | L | E |
| A | L | E | S |
| T | E | S | T |
Breaks and Never Falls
What breaks and never falls, and what falls and never breaks?
SOLUTION
Day breaks and night falls.
Ten Matchsticks
You have these fifteen matchsticks. Remove six of them and leave ten.
SOLUTION
Remove 6 matchsticks and leave 9 that spell the word TEN.
Washing Dishes
A man is alone in his house washing dishes. When he looks down, there are more glasses in the sink than there were before. How come?
SOLUTION
The man’s pair of glasses fell inside the sink.
Frustrating Question
John was asking Bob the same question again and again throughout the day and kept getting different answers. What was John’s question?
SOLUTION
John’s question was “What time is it?”.
Splitting Coins
You split 1000 coins into two piles and count the number of coins in each pile. If there are X coins in pile one and Y coins in pile two, you multiple the two numbers to get XY. Then you split both piles further, repeating the same counting and multiplication process, and adding the new multiplication results to the first one. The process ends when you end up with 1000 single-coin piles. Prove that you will always get the same final result, no matter how the piles have been divided during the splitting process.
For example, if you start with 5 coins and split them into a pile of 2 and a pile of 3, you get the number 2×3=6. Then, if you split the pile of 3 into a pile of 1 and a pile of 2, you will add 1×2=2 more to the 6 and get 8. Finally, if you split the two piles of 2 into single-coin piles, you will end up with 8+1+1=10.
SOLUTION
Consider the sum of the squares of the numbers of coins in each pile, plus twice the sum of the products. On each step, if you split a pile of X+Y coins into a pile of X coins and a pile of Y coins, the sum of the squares will get reduced by 2XY, exactly the amount the sum of the products will increase by. Therefore, that number remains constant throughout the entire process and ends up exactly (1000²-1000)/2=499500.
1 to 8 on a Cube
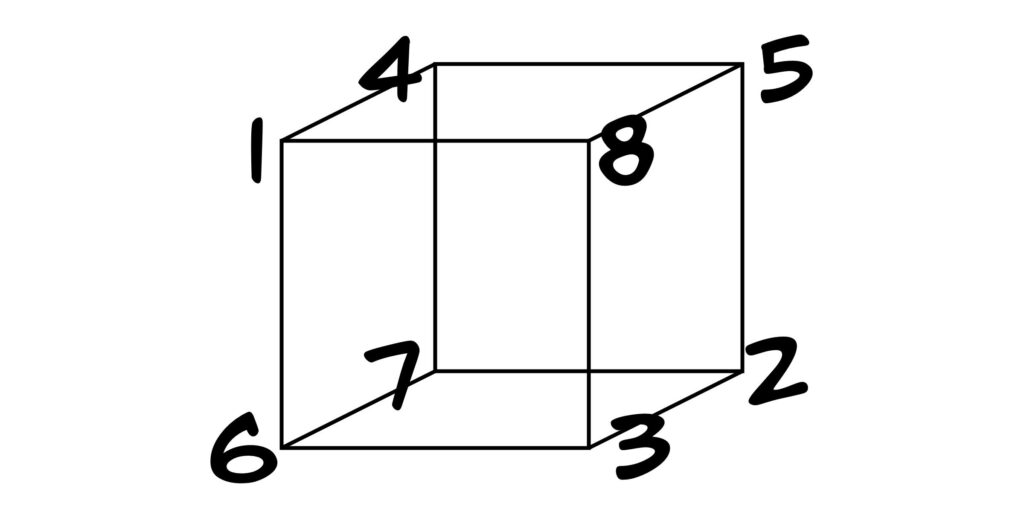
Place the numbers from 1 to 8 on the vertices of a cube so that the sum of the four numbers on every face is the same.
SOLUTION
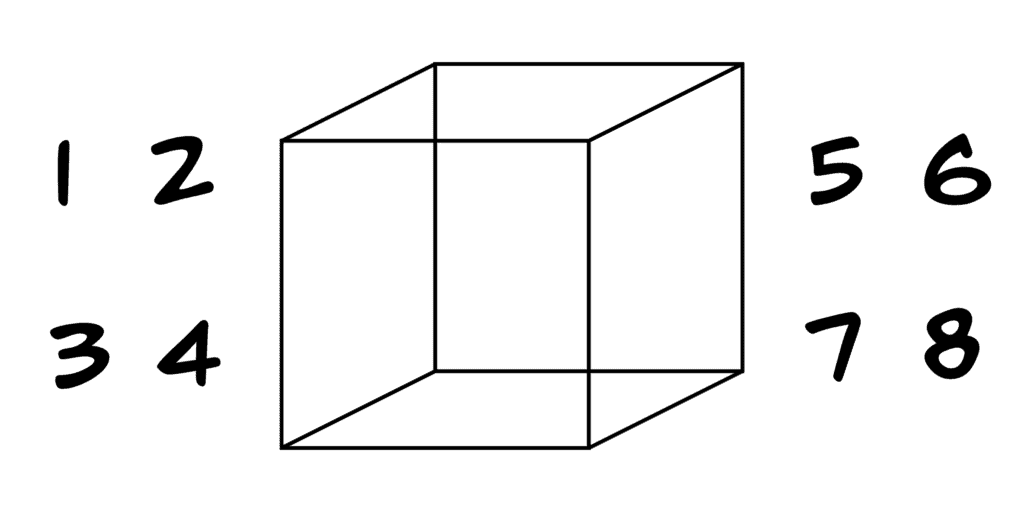
The solution is shown below:
