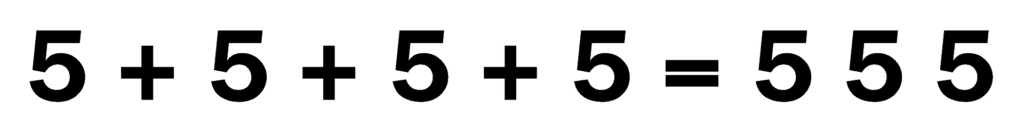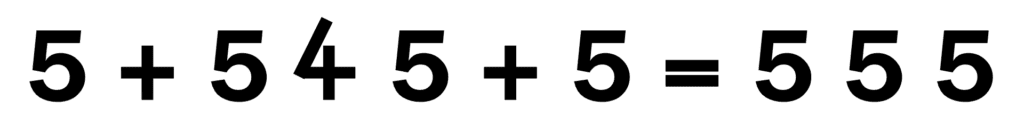We do not know where this puzzle originated from. If you have any information, please let us know via email.
The police found a murdered man in a car. The windows of the car were raised, the doors were locked, and the keys were inside, in the man’s hands. The man was shot several times with a gun, but there were no holes anywhere on the car. How is this possible?
The car was convertible, with the top retracted back.
Add just one line to create a correct equality.
Add a line to the plus to transform it into a four.
100 prisoners are given the following challenge: They will be taken to a room and will be arranged in a column, such that each of them faces the backs of the prisoners in front. After that, black and red hats will be placed on their heads, and the prisoners will be asked one at a time what is the color of their hat, starting from the one at the back of the column. If a prisoner guesses his color correctly, he is spared; if not – he is executed. If every prisoner can see only the hats of the prisoners in front of him in the line, what strategy should they come up with, so that their losses are minimized?
There is a strategy which ensures that 99 prisoners are spared and there is 50% chance that one of them is executed. Clearly, one can not do better.
The strategy is as follows: The first prisoner (at the back of the line) counts the number of black hats worn by the prisoners in front. If the number is odd, he says “BLACK”. If the number is even, he says “RED”. Then, the second prisoner counts the black hats in front of him, figures out the color of his own hat, and answers the question.The third prisoner sees the number of black hats in front of him and uses this information, along with what the second prisoner’s hat is, to determine the color of his own hat. The prisoners continue in the same manner until all 99 prisoners in the front guess their hat colors correctly. The chance for survival of the first prisoner is 50%.
John is talking to his lawyer in jail. Both of them are very upset
John was visiting his lawyer who was the one in jail.
Prepare a piece of paper with dimensions 2×4, then fold it four times to form 8 squares. Write on the squares in the top row the numbers 1, 8, 7, 4, and write on the squares in the bottom row the numbers 2, 3, 6, 5.
Now your task is to fold the piece of paper several times, so that the squares end up on top of each other, with the numbers appearing in ascending order top to bottom, and 1 face up.
Once you do this, try again with numbers 1, 8, 2, 7 on the top row, and 4, 5, 3, 6 on the bottom row.
Coming soon.
A woman shoots her husband, then holds him under water for five minutes, then hangs him, and finally
The woman takes a picture of her husband and develops it in a dark room.
Two gunshots were fired through the window of a coffee shop. When the police arrived, they successfully recognized which gunshot was fired first. Which was the first gunshot and how did they figure that out?
The cracks of the left gunshot end up right at the cracks of the right gunshot. Therefore the first gunshot is the one on the right.
Can you draw uncountable many non-intersecting “8” shapes in the plane (they can be contained in one another)?
No, you can’t. For each “8” shape you can choose a pair of points with rational coordinates – one in its top loop and one in its bottom loop. Since no two “8” shapes can have the same corresponding pair of rational points, their number should be countable.
A prince decides to get married to the prettiest girl in his kingdom. All 100 available ladies go to the palace and show themselves to the prince one by one. He can either decide to marry the girl in front of him or ask her to leave forever and call the next one in line. Can you find a strategy which will give the prince a chance of 25% to get married to the prettiest girl? Can you find the best strategy?
Remark: Assume that the prince can objectively compare every two girls he has seen.
A strategy which ensures a chance of 25% is the following:
The prince banishes the first 50 girls which enter the palace and then gets married to the first one which is prettier than all of them (if such one arrives). If the prettiest girl in the kingdom is in the second 50, and the second prettiest girl is in the first 50, he will succeed. The chance for this is exactly 25%.
The best strategy is to wait until ~1/e of all girls pass, and then choose the first one which is more beautiful than all of them. This yields a chance of ~37% for succeeding. The proof is coming soon.
Take six coins and arrange them in a triangle as shown in the image. Your goal is to rearrange the coins into a hexagon with only four moves. Every move consists of sliding one coin to a new location where it touches at least two other coins.
The solution is shown below.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.
