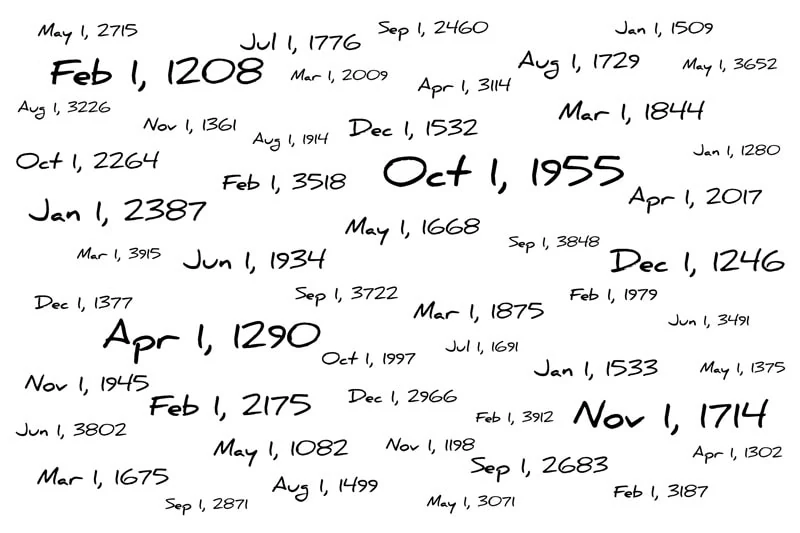Category: Rebus
Thoka’s Rebus 3
Can you figure out which phrase is depicted by this rebus?

The first image on the first row depicts a BALL. The second image depicts a BROOM which is removing the B, so you end up with BALL+ROOM=BALLROOM.
The first image on the second row depicts TOES, and the second image on the second row transforms the first letter T to a silent SH. Therefore, the final answer is BALLROOM SHOES.
Thoka’s Rebus 2
Can you figure out which word is depicted by this rebus?

The first image depicts a SEA. When you switch the third letter to C, you get SEC. The second image depicts RED. When you make the third letter a hard consonant, you get RET. The last two images depict a DIARY and DI (501 in Roman numerals). Therefore, you get:
SEC + RET + DIARY – DI = SECRETARY
Thoka’s Rebus 1
Can you figure out which word is depicted by this rebus?

Each of the images in the first row depicts HAIR. Each of the images in the second row (except the second cell) depicts a BUG. Each of the images in the third row depicts ER.
The I from HAIR on the first row gets moved right after the B from BUG on the second row. Also, the U from BUG gets flipped upside down. Therefore, we get HARBINGER.
Puzzle Sum 24
What animal does this sum spell?

TURK + EEL – KEEL + BEETLE – BEE = TURTLE
Puzzle Sum 23
What animal does this sum spell?

BAG + LASS – GLASS + TRACK – RACK = BAT