Puzzles 29 - Puzzle Prime

Beautiful Tapestry

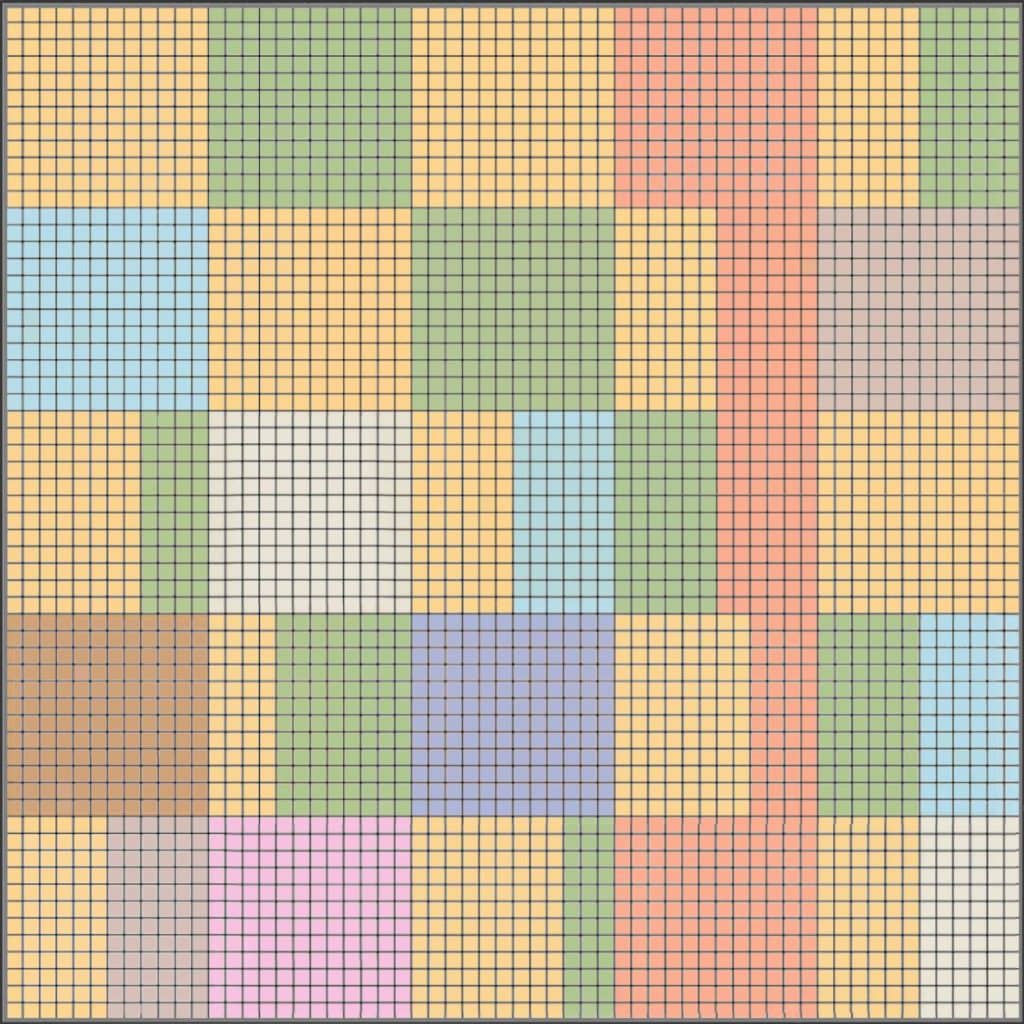
Section: Brain Teasers Category: Mathematics

Difficulty: Advanced

A piece of a beautiful tapestry is missing. Can you figure out what its colors are?

SOLUTION

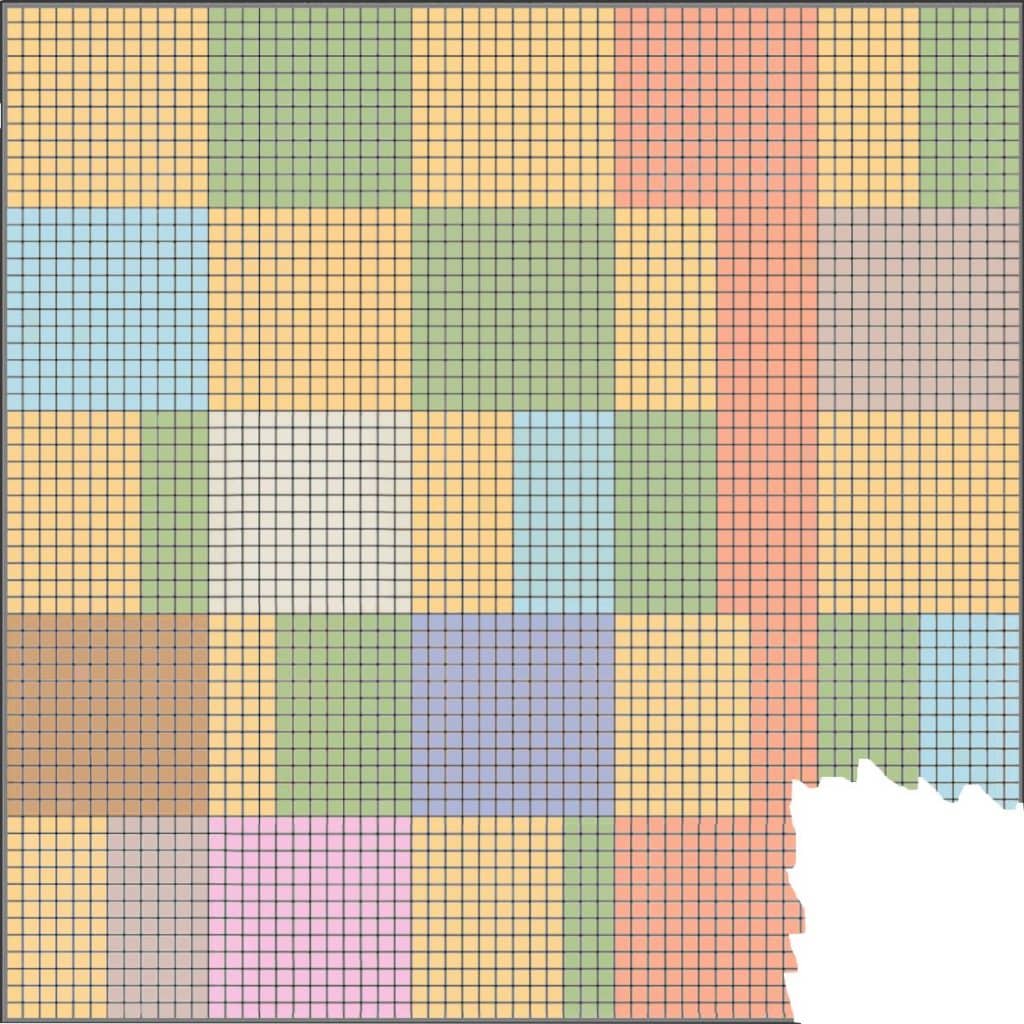
The tapestry represents the factorizations of the numbers from 2 to 26.

Each 12×12 square on the tapestry represents a number between 2 and 26, such that all squares representing prime numbers are painted in single colors. The colors of the squares representing composite numbers are determined by the factors of these numbers.

The number 2 is represented by orange color (top left corner). The number 3 is represented by green color. The number 4 = 2×2 is represented once again by orange (2, 2) color. The number 5 is represented by red color. The number 6 = 2×3 is represented by orange (2) and green (3) colors. The number 7 is represented by blue color. The number 8 = 2×2×2 is represented once again by orange (2, 2, 2) color. The number 9 =3×3 is represented once again by green (3, 3) color. The number 10 = 2×5 is represented by orange (2) and red (5) colors, and so on.

Unknown Author September 19, 2021

0 Comments

Scratch My Head

Section: Casual Puzzles Category: Riddle

Difficulty: Easy

Tear one off and scratch my head,
What once was red is black instead.

What is it?

SOLUTION

The answer is MATCHSTICK.

The Riddler September 16, 2021

2 Comments

FEATURED

Does Not Divide Another

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Featured

How many numbers between 1 and 100 can you pick at most, so that none of them divide another?

SOLUTION

You can choose fifty numbers at most: 51, 52, 53, … , 100.

In order to see that you cannot choose more than fifty, express each number in the form 2ⁿ×m, where m is an odd number. Since no two numbers can have the same m in their expressions, and there are only fifty odd numbers between 1 and 100, the statement of the problem follows.

Unknown Author September 13, 2021

1 Comment

Big on Saturday

Section: Casual Puzzles Category: Riddle

Difficulty: Medium

I am big on Saturday and Sunday.
I am small on Tuesday, Wednesday, and Thursday.
I am not on Monday and Friday.

What am I?

SOLUTION

The answer is the letter S.

Unknown Author September 10, 2021

1 Comment

Surrounded by Rooks

Section: Brain Teasers Category: Chess

Difficulty: Medium

White to play and mate Black in 20 moves.

SOLUTION

The moves are as follows:

Qb7+ Rc5c6
Qa5+ Rc4c5
Qb3+ Rd4c4
Qd2+ Re4d4
Qf3+ Re5e4
Qg5+ e5
Qf7+ Rd6e6
Qd8+ Rc6d6
Qb7+ Rc5c6
Qa5+ Rc4c5
Qb3+ Rd4c4
Qd2+ Re4d4
Qf3+ e4
Qg5+ Re6e5
Qf7+ Rd6e6
Qd8+ Rc6d6
Qb7+ Rc5c6
Qa5+ Rc4c5
Qb3+ Rd4c4
Qd2x

Unknown Author September 7, 2021

2 Comments

Murder Mystery Puzzles

Section: Brain Teasers Category: Deduction

Difficulty: Advanced

In the three murder cases below, you can read the testimonies of all suspects. For each case, find who the killer is, knowing that no 2 people are in the same row or column, and that the killer was alone in a room with the victim.

SOLUTION

The solutions are shown below.

Hiroji Osaka September 1, 2021

1 Comment

Murdered Wife

Section: Brain Teasers Category: Lateral

Difficulty: Medium

One night, a man received a call from the Police. The Police told the man that his wife was murdered, and that he should get to the crime scene as soon as possible. The man immediately hung up the phone and drove his car for 20 minutes. As soon as he got to the crime scene, the Police arrested him, and he got convicted for murder.

How did the Police know that the man committed the crime?

SOLUTION

The police did not tell the man where the crime scene was.

Unknown Author August 28, 2021

0 Comments

What Does the Liаr Do

Section: Casual Puzzles Category: Riddle

Difficulty: Easy

What does the liar do when he dies?

SOLUTION

He lies still.

Unknown Author August 25, 2021

2 Comments

Self-Describing Number

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced

Find all 10-digit numbers with the following property:

the first digit shows the number of 0s in the number
the second digit shows the number of 1s in the number
the third digit shows the number of 2s in the number, and so on

SOLUTION

Let the number be ABCDEFGHIJ. The number of all digits is 10:

A + B + C + D + E + F + G + H + I + J = 10

Therefore, the sum of all digits is 10. Then:

0×A + 1×B + 2×C + 3×D + 4×E + 5×F + 6×G + 7×H + 8×I + 9×J = 10

We see that F, G, H, I, J < 2. If H = 1, I = 1, or J = 1, then the number contains at least 7 identical digits, clearly 0s. We find A > 6 and E = F = G = 0. It is easy to see that this does not lead to solutions, and then H = I = J = 0.

If G = 1, we get E = F = 0. There is a 6 in the number, so it must be A. We get 6BCD001000, and easily find the solution 6210001000.

If G = 0, F can be 0 or 1. If F = 1, then there must be a 5 in the number, so it must be A. We get 5BCDE10000. We don’t find any solutions.

If F = 0, then the number has at least five 0s, and therefore A > 4. However, since F = G = H = I = J = 0, the number does not have any digits larger than 4, and we get a contradiction.

Thus, the only solution is 6210001000.

Unknown Author August 19, 2021

3 Comments

FEATURED

Five Points in a Square

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Featured

There are 5 points in a square 1×1. Show that 2 of the points are within distance 0.75.

SOLUTION

Split the unit square into 4 small squares with side lengths 0.5. At least one of these squares will contain 2 of the points. Since the diagonals of the small squares have lengths less than 0.75, these 2 points must be within such distance.

Unknown Author August 16, 2021

6 Comments