FEATURED
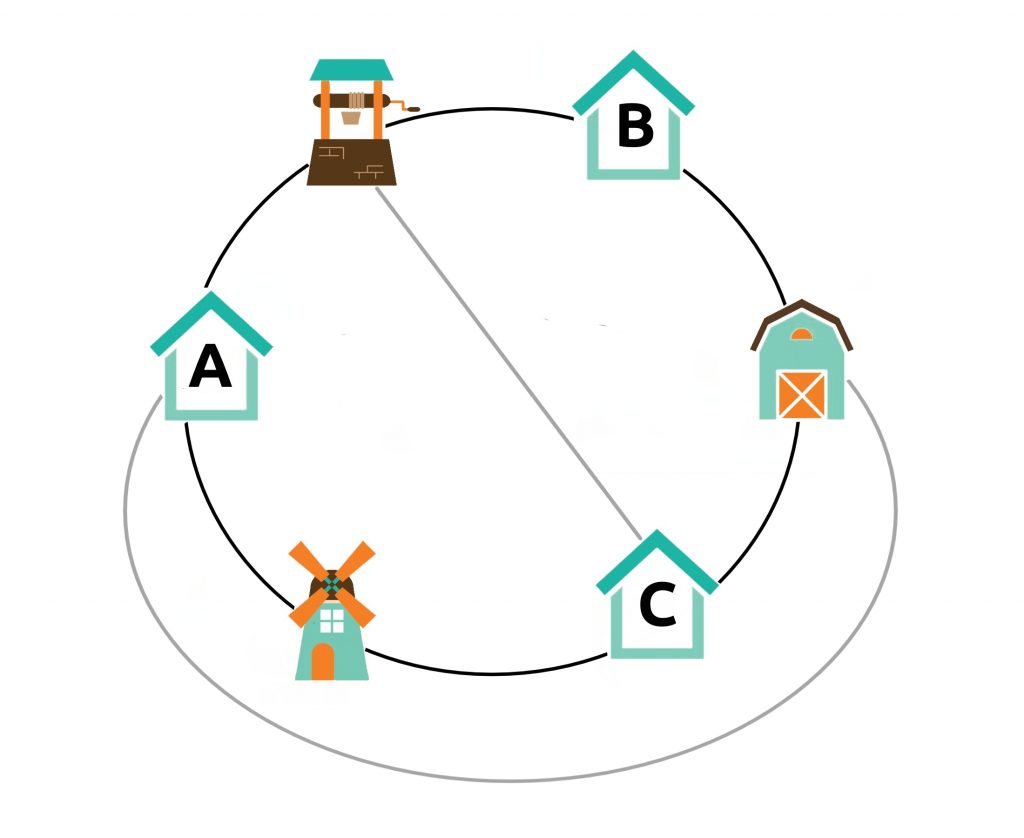
Houses on a Farm
Is it possible to connect each of the houses with the well, the barn, and the mill, so that no two connections intersect each other?
SOLUTION
Category: Puzzles
We do not know where this puzzle originated from. If you have any information, please let us know via email.
FEATURED
Game of Coins
Kuku and Pipi decide to play a game. They arrange 50 coins in a line on the table, with various nominations. Then, alternating, each player takes on their turn one of the two coins at the ends of the line and keeps it. Kuku and Pipi continue doing this, until after the 50th move all coins are taken. Prove that whoever starts first can always collect coins with at least as much value as their opponent.
Remark: On the first turn, Kuku can pick either coin #1 or coin #50. If Kuku picks coin #1, then Pipi can pick on her turn either coin #2 or coin #50. If Kuku picks coin #50, then Pipi can pick on her turn either coin #1 or coin #49.
SOLUTION
Two Trains and a Bridge
Two trains are crossing the bridge bellow at the same speed on a non-windy day. One of the trains
SOLUTION
Chess Peace
Can you add all 16 black pieces on the board (king, queen, 2 knights, 2 bishops, 2 rooks, 8 pawns) and get a chess position, in which no piece is attacked by another?
SOLUTION
Three Cards
There are three playing cards in a row. There is a two to the right of a king. There is a diamond to the left of a spade. There is an ace to the left of a heart. There is a heart to the left of a spade. Identify the three cards.
SOLUTION
FEATURED
Cheryl’s Birthday
Cheryl’s birthday is one of 10 possible dates:
May 15
May 16
May 19
June 17
June 18
July 14
July 16
August 14
August 15
August 17
Cheryl tells the month to Albert and the day to Bernard.
Albert: I don’t know the birthday, but I know Bernard doesn’t know either.
Bernard: I didn’t know at first, but now I do know.
Albert: Now I also know Cheryl’s birthday.
When is Cheryl’s birthday?
SOLUTION
Perfect Day
Dear Diary,
This morning, I woke up at 9 o’clock. My first job was to drink a glass of water and brush my teeth. After that, I ate an apple, 2 bananas, and a toast with almond butter for breakfast. Then, I went to the gym for one hour, took a shower, and came back home at eleven. I cooked a few pieces of chicken with sweet potatoes for lunch; ate everything. In the afternoon, I started working on my projects while listening to classical music. In the evening, I went for the 2nd time to the gym, did cardio for half-an-hour, and after that visited my friend’s apartment. We had together one big pizza for dinner and in the end, I fell asleep on his couch.
As you can see, my entire day was perfect, except that my laptop keyboard broke. Can you figure out what’s wrong with it?
SOLUTION
FEATURED
Puzzle Tournament 2
Puzzle Prime’s second puzzle tournament was organized on June 27, 2020. Congrats to Elyot G. who solved all the puzzles! You can see the problems and the rankings below.
You have 60 minutes to solve 6 puzzles, each worth 1 point. Upload your solutions as a pdf, document, or image, using the form below. Good luck!
Time for work: 1 hour
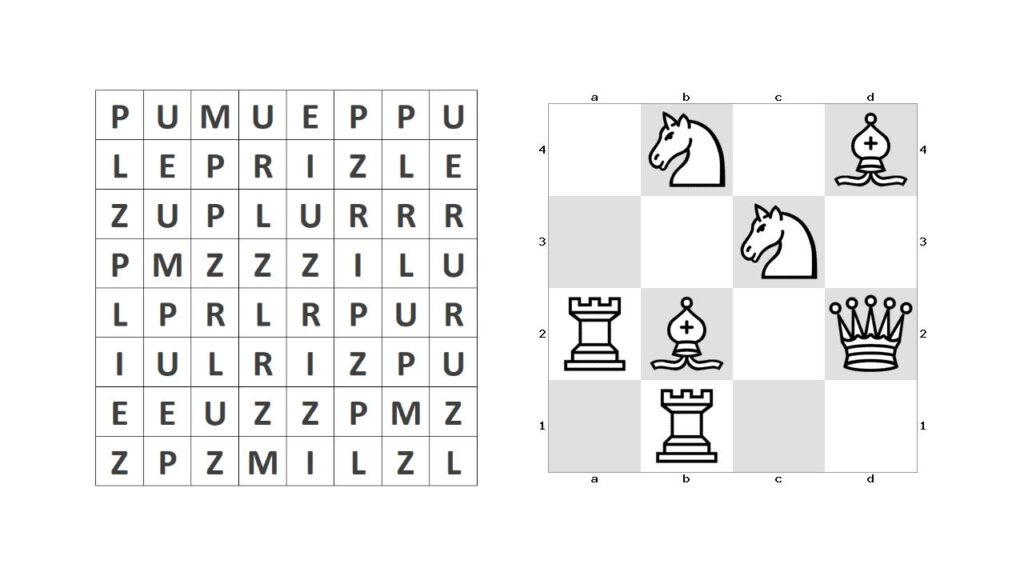
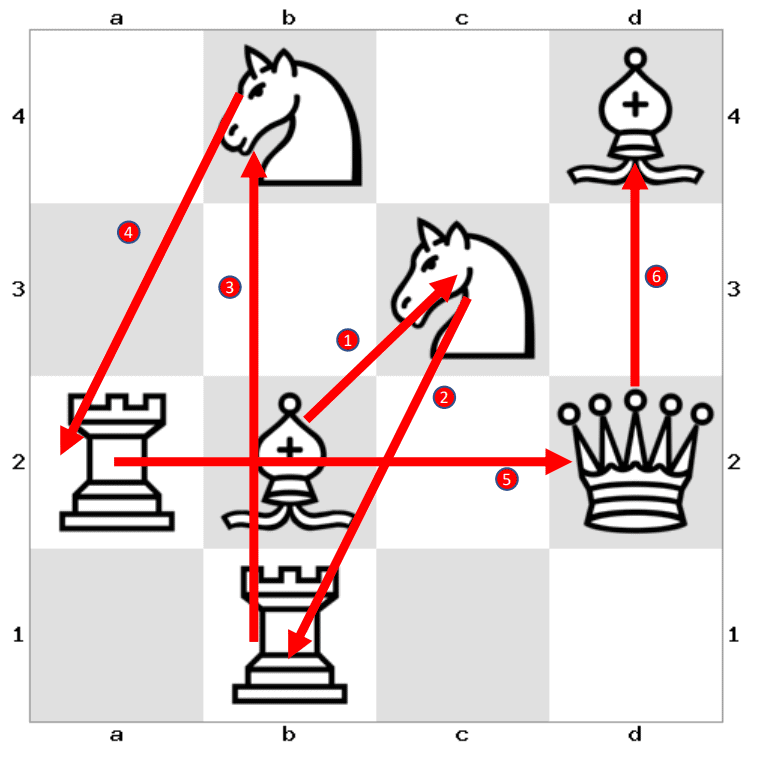
Puzzle Prime Knight
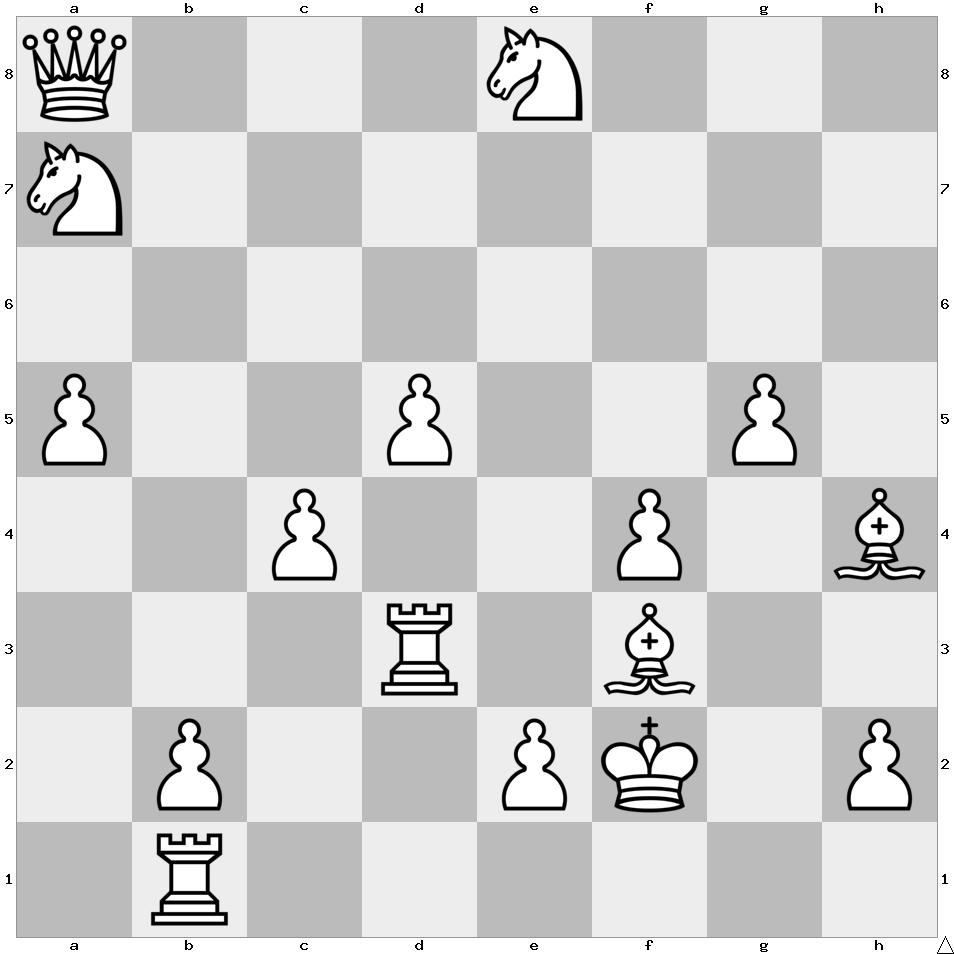
Start from a square with a P on the chessboard, and keep jumping via knight’s move, consequently landing on squares with the letters U-Z-Z-L-E-P-R-I-M-E.
Point of View
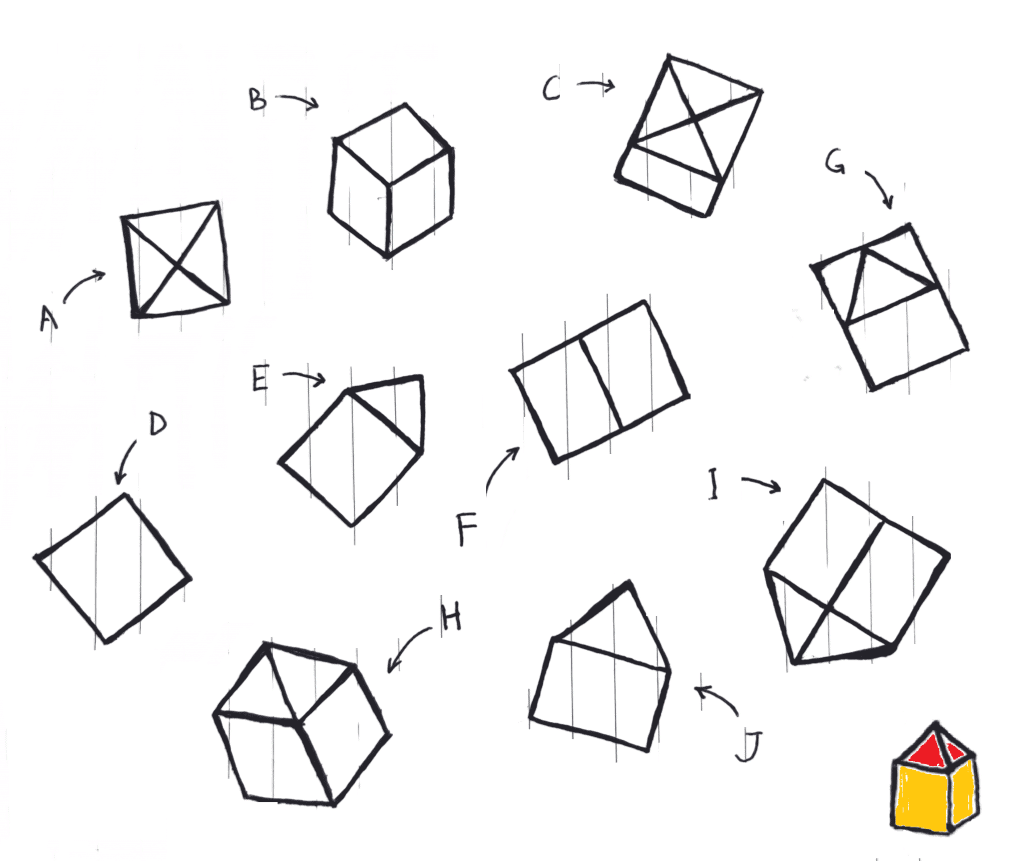
8 of these diagrams correspond to views of the object in the corner when it is looked from different perspectives. Which 2 aren’t?
Note: The projections below are parallel (not perspective).
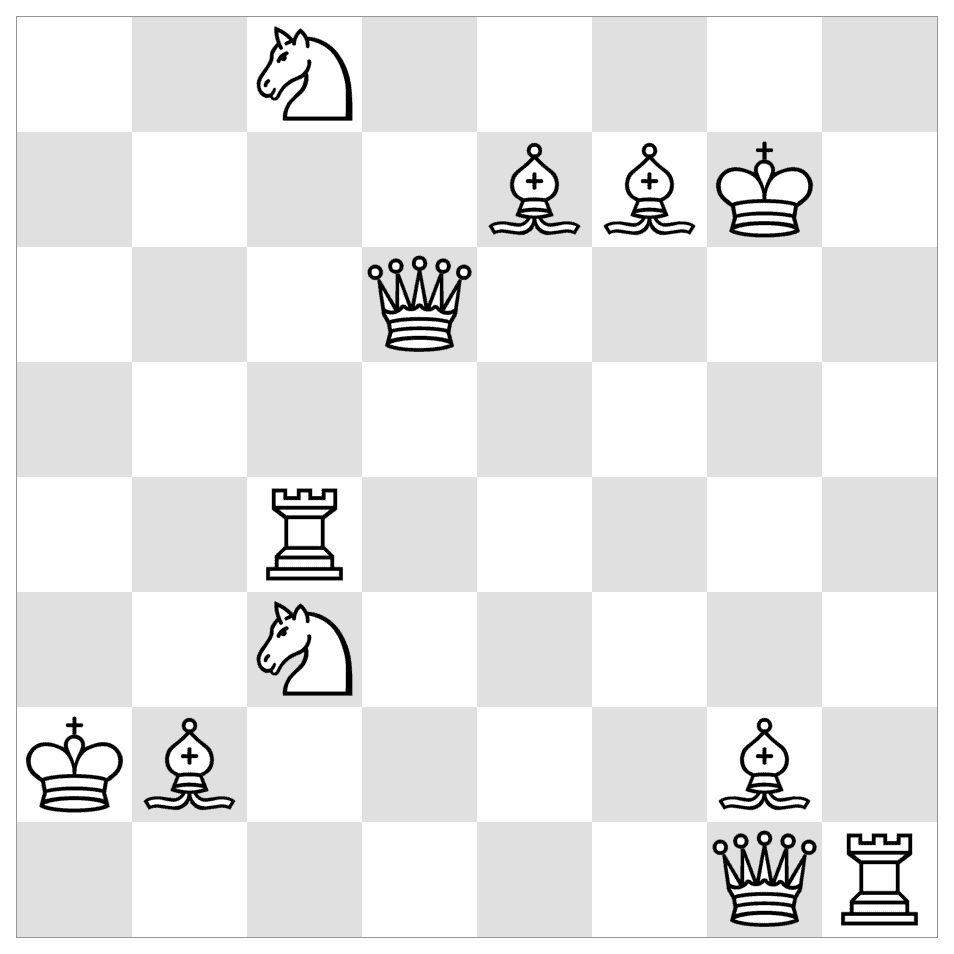
Chess Fight
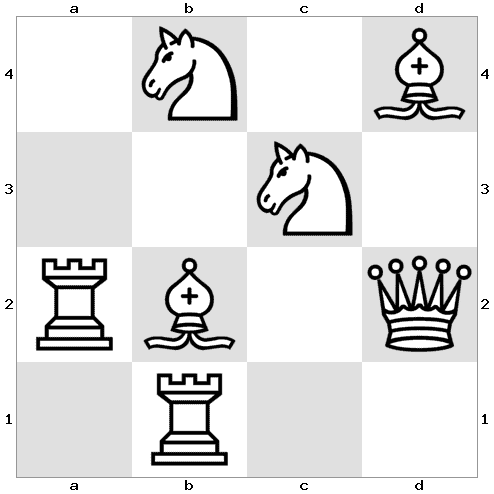
Choose a chess piece on the board. Then, move the piece to a cell with another piece, and remove the first piece. Repeat, by moving the second piece to a cell with a new piece, and removing it. Continue until there is only one piece remaining on the board.
Note: For example, we can move the Queen on d2 to the Bishop on b2, the Knight on c3, or the Bishop on d4. If we move the Queen to d4 and remove it from the board, then we must move the Bishop on d4. The only available cell is c3, where a Knight is positioned. We must remove the bishop and move the Knight on c3 either to the Rook on b1 or the Rook on a2…
Special Date
On April 5, 2013 (5.4.2013), the digits used for expressing the date were all different and consecutive. When was the last date before it with this property?
Remark: The digits 9 and 0 are not consecutive.
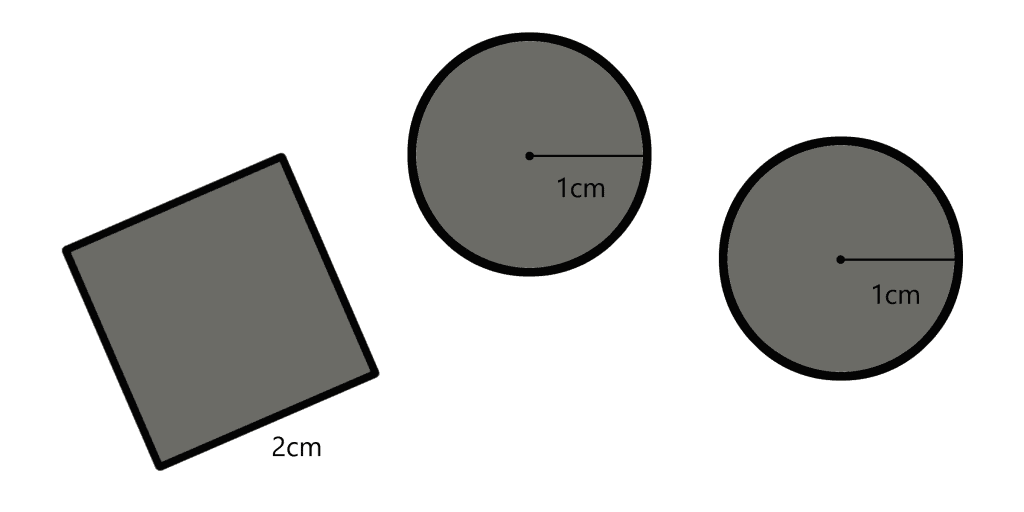
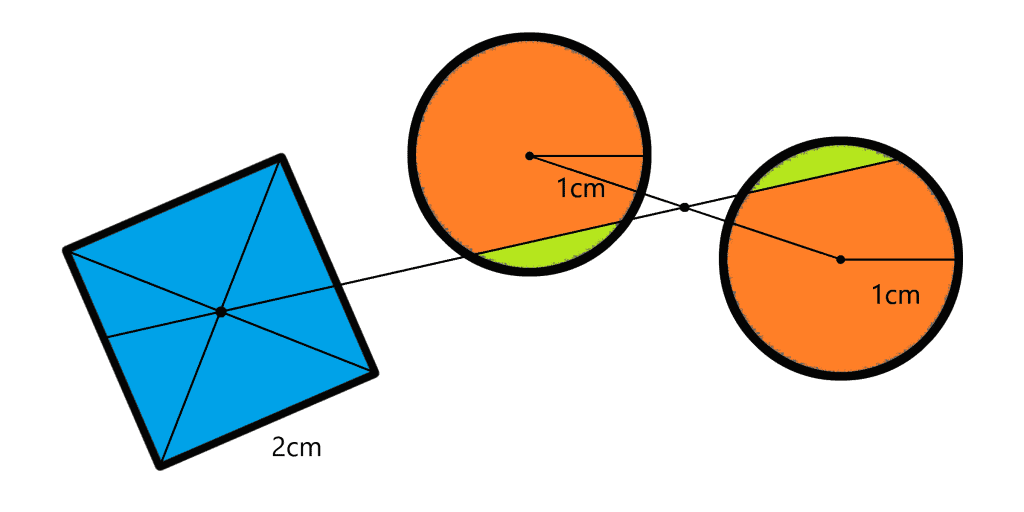
Splitting the Area
You have 1 square with side length 1 and 2 circles with diameter length 1. Draw a single line so that the resulting areas on the left and on the right of the line are equal.
Notes: You need to specify how you find a line satisfying the condition above.
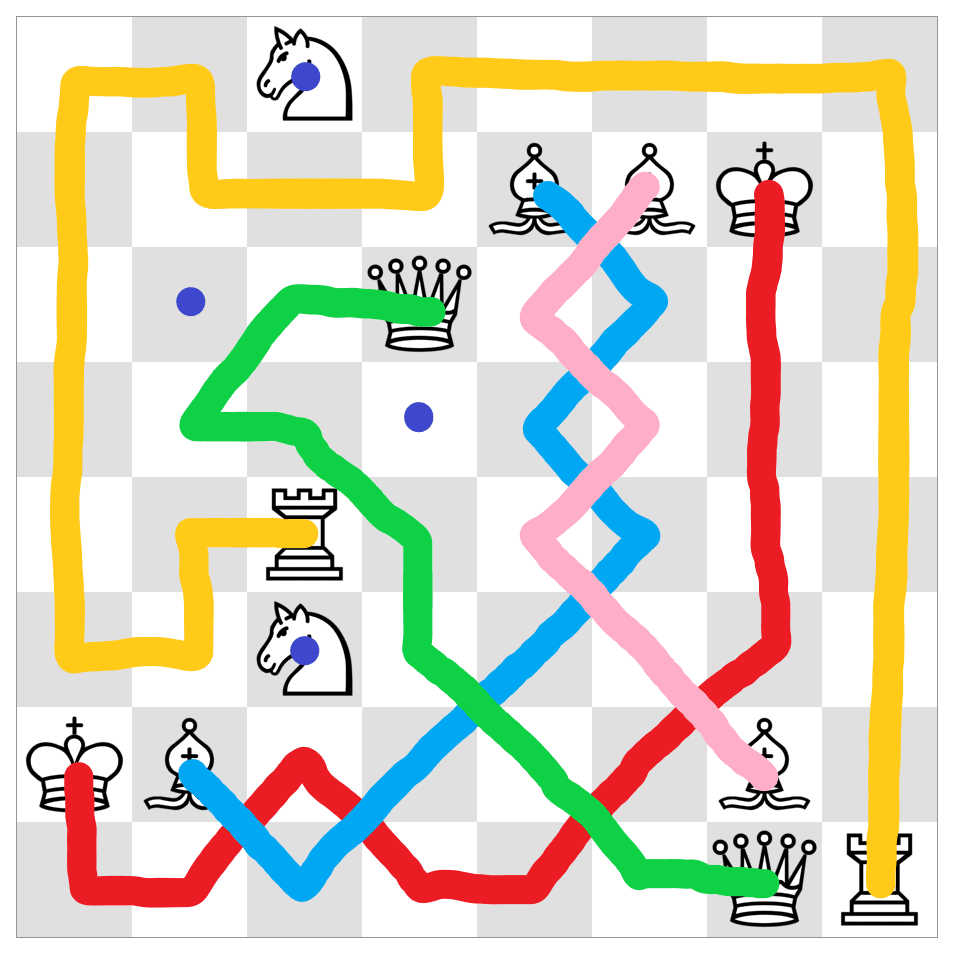
Chess Connect
The starting and ending positions of 6 chess pieces are shown on the board. Find the trajectories of the pieces, if you know that they do not overlap and completely cover the board.
Notes: The pieces can not backtrack. Two trajectories can intersect diagonally but can not pass through the same square. Only the Knight has a discontinuous trajectory.
Solutions
The answer to Point of View is C and J.
The answer to Special Date is 23.4.1765.
The solutions of the other puzzles are shown below.
Results
| Puzzler | P1 | P2 | P3 | P4 | P5 | P6 | Total |
|---|---|---|---|---|---|---|---|
| Elyot G. | 1 | 1 | 1 | 1 | 1 | 1 | 6 |
| David R. | 1 | 0 | 1 | 0 | 1 | 1 | 4 |
| Rodrigo R. | 1 | 0.5 | 1 | 0 | 0 | 1 | 3.5 |
| N | 1 | 0 | 1 | 0 | 1 | 0 | 3 |
| Hristo H. | 0 | 0 | 1 | 0 | 1 | 0 | 2 |
| Rockmosis | 1 | 0 | 1 | 0 | 0 | 0 | 2 |
Prizes
#1.
$10 Gift Card (iTunes or Play Store)
Puzzle Avatar (custom made)
Puzzle Pelago (mobile game by Hallgrim Games)
Hook (mobile game by Rainbow Train)
#2.
$5 Gift Card (iTunes or Play Store)
Puzzle Avatar (custom made)
Puzzle Pelago (mobile game by Hallgrim Games)
Hook (mobile game by Rainbow Train)
#3.
Puzzle Avatar (custom made)
Puzzle Pelago (mobile game by Hallgrim Games)
Hook (mobile game by Rainbow Train)
#4-5.
Puzzle Pelago (mobile game by Hallgrim Games)
Hook (mobile game by Rainbow Train)
