Hard – Page 10 – Puzzle Prime

FEATURED

Tetris Maze

Section: Casual Puzzles Category: Maze

Difficulty: Hard Tags: Featured

In order to catch the thief, you must make your way through this Tetris maze formed by the 5 different pieces shown at the bottom. You can not climb over the blocks, just find a tunnel inside the construction.

SOLUTION

The solution is shown below.

Johann Sturcz May 11, 2018

0 Comments

Beat Strata

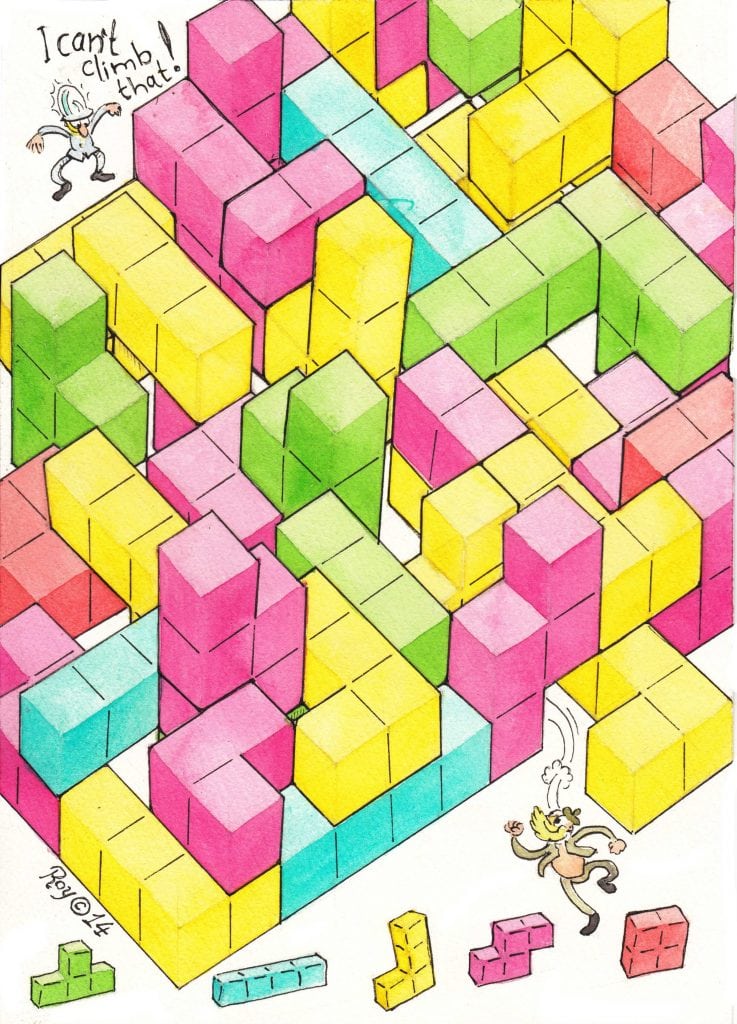
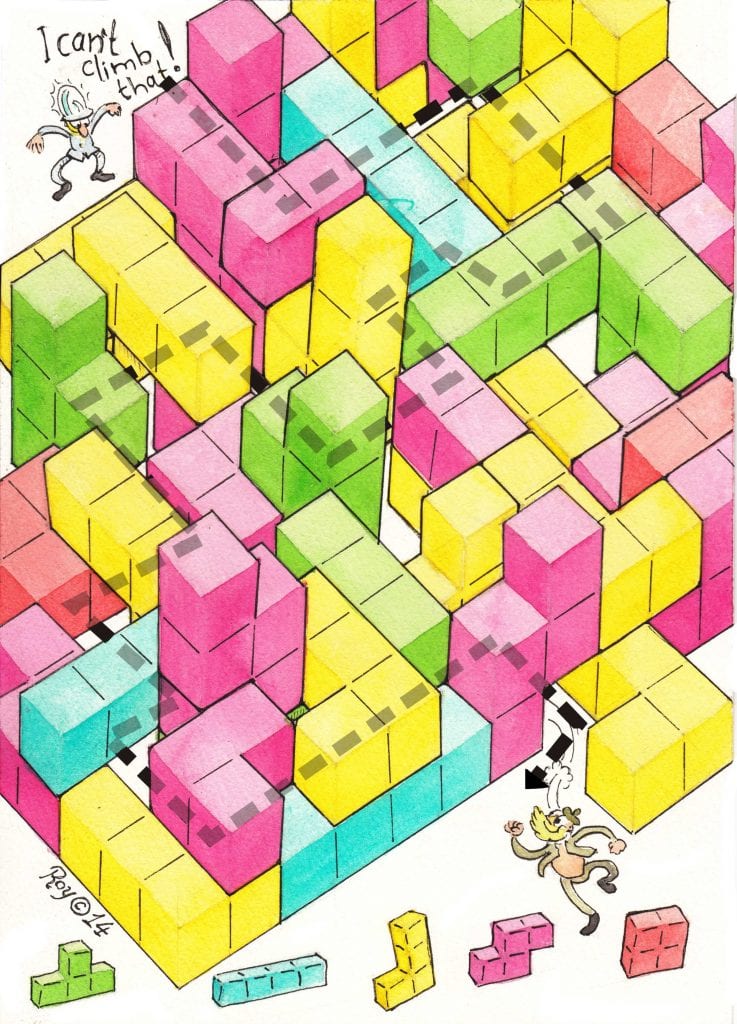
Section: Brain Teasers Category: Insight

Difficulty: Hard

Strata is a beautiful award-winning game with mesmerizing sound and unique puzzle concept. It contains hundreds of levels with common rules and final goal. Below I present you these rules and ask you to find a universal algorithm, which will allow you to solve easily every single level of the game.

The rules are simple – you begin with an nxn board, some squares of which are colored in arbitrary colors. Then you start placing stripes of whatever color you choose over entire rows and columns of the board. Your task is after placing all available 2n stripes, the color of every (colored) square to match the color of the stripe which has been placed second over it (on top).

Can you find a simple algorithm, which results in solving any level of the game, no matter the starting position? You can watch AppSpy’s video below for better understanding of the rules.

SOLUTION

Imagine the reverse Strata puzzle – the color of every square must match the color of the first stripe which is placed upon it. Clearly, there must be a line in the grid such that all colored squares in it have the same color. Take all such lines in the grid and place on them stripes of appropriate colors. Then erase the colors from all squares covered by the stripes and repeat the procedure until you place all 2n stripes. It is easy to see that if the reverse Strata puzzle has a solution, then we will find it using this strategy. Finally, in order to solve the original Strata puzzle, just place the stripes in reverse order.

Puzzle Prime April 13, 2018

0 Comments

The Rotating Square

Section: Brain Teasers Category: Insight

Difficulty: Hard

On the table in front of you there is a square with 4 coins placed on its vertices. You are blindfolded and are given the task to turn all of the coins with either heads up or tails up. Every time you turn few of the coins however, the square rotates arbitrarily on the table. Find a strategy, such that no matter the starting arrangement of the coins and no matter how the square rotates after every flip of coins, eventually you will turn all of the coins with the same face up.

SOLUTION

First assume that there is even number of tails and even number of heads on the table – 2 of each kind. Flip 2 opposite coins. If after that not all coins have the same face up, the coins’ faces along the square’s corners show T-T-H-H. Now flip 2 adjacent coins. If after that not all coins have the same face up, the coins’ faces along the square’s corners show T-H-T-H. Now flip again 2 opposite coins and you are done.

Next assume that there were intially odd number of tails and odd number of heads on the table. Then after applying the moves described above, flip one of the coins upside down. Now there is even number of heads and even number of tails on the table, so you can repeat the same procedure and accomplish the task.

Unknown Author March 28, 2018

2 Comments

Students with Hats

Section: Brain Teasers Category: Deduction

Difficulty: Hard

Professor Vivek decided to test three of his students, Frank, Gary and Henry. The teacher took three hats, wrote on each hat a positive integer, and put the hats on the heads of the students. Each student could see the numbers written on the hats of the other two students but not the number written on his own hat.

The teacher said that one of the numbers is sum of the other two and started asking the students:

— Frank, do you know the number on your hat?
— No, I don’t.
— Gary, do you know the number on your hat?
— No, I don’t.
— Henry, do you know the number on your hat?
— Yes, my number is 5.

What were the numbers which the teacher wrote on the hats?

SOLUTION

The numbers are 2, 3, and 5. First, we check that these numbers work.

Indeed, Frank would not be able to figure out whether his number is 2 or 8. Then, Gary would not be able to figure out whether his number is 3 or 7, since with numbers 2, 7, 5, Frank still would not have been able to figure his number out. Finally, Henry can conclude that his number is 5, because if it was 1, then Gary would have been able to conclude that his number is 3, due to Frank’s inability to figure his number out.

Next, we we check that there are no other solutions. We note that if the numbers are 1, 4, 3, or 3, 2, 1, or 4, 1, 3, neither Frank nor Gary would have been able to figure their number out. Therefore, if the numbers were 1, 4, 5, or 3, 2, 5, or 4, 1, 5, Henry would not have been able to figure his number out. Thus, 5 is not the largest number.

Similarly, if the numbers are X, X + 5, X + 10, or X + 5, X, X + 10, once again, neither Frank nor Gary would have been able to figure their number out. Therefore, if the numbers were X, X + 5, 5, or X + 5, X, 5, Henry would not have been able to figure his number out.

Unknown Author March 20, 2018

2 Comments

Strips in the Plane

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

Prove that you can not cover the plane with infinite strips which have a total sum of their widths equal to 1.

SOLUTION

Take a circle with radius 1 in the plane. A strip with width X covers at most an area of 2X of the circle. Therefore all strips cover at most an area of 2, which is smaller than the total area of the circle (~3.14).

Unknown Author February 17, 2018

0 Comments

Shuffling Cards

Section: Brain Teasers Category: Insight

Difficulty: Hard

52 cards – 2 of clubs to Ace of clubs, 2 of diamonds to Ace of diamonds, 2 of hearts to Ace of hearts, and 2 of spades to Ace of spades – are arranged in a deck. We shuffle them in the following manner:

We take the top card and put in a random place inside the deck.
Once we get to the King of spades and put it somewhere in the deck, we stop.

Show that this method shuffles the deck uniformly, i.e. every permutation has the same chance to appear.

SOLUTION

Notice that at all times the cards below the King of spades are shuffled uniformly. Therefore at the end, after we put the King of spades in a random place inside the deck, the entire shuffle will be uniform as well.

Puzzle Prime February 12, 2018

0 Comments

Integers on a Chess Board

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

You are given an 8×8 chess-board, and in each of its cells, there is written one integer. If the difference between any two adjacent numbers is -1, 0 or 1, prove that some number is repeated at least 8 times on the board.

SOLUTION

Consider the intervals spanned by the numbers in the first row, second row, third row, etc. If all of these intervals intersect each other, then there is a number, which appears in all of them. If not, there are two intervals, which are disjoint, and a number between them, which does not appear in the two rows. Now it is easy to see that this particular number will appear in every column.

Unknown Author January 22, 2018

0 Comments

Game of Chess

Section: Brain Teasers Category: Chess

Difficulty: Hard

Ned and Jon are playing chess. Eventually, they end up in a position in which Ned (whites) is left with 2 rooks, and Jon (blacks) has just his king on the board. If Ned can mate Jon in exactly 4 different ways, what is the position of the pieces?

SOLUTION

Black king on a1, white king on e1, white rooks on c2 and h1. Ned hasn’t moved his king and rook, so he can either castle or move his king to d2, e2 or f2, resulting in a mate.

Unknown Author January 20, 2018

0 Comments

Lost Boarding Pass

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Probability

There are 100 passengers which are trying to get on a plane. The first passenger, however, has lost his boarding pass, so decides to sit on an arbitrary seat. Each successive passenger either sits on his own seat if it is empty or on an arbitrary other if it is taken. What is the chance that the last person will sit in his own seat?

SOLUTION

The chance is 50%. Indeed, the last passenger will either have to sit in his own seat or the one which belongs to the first passenger. Since there hasn’t been any preference made by anyone at any time towards any of these two seats, the probability that either of them is left last is 1/2.

Puzzle Prime December 16, 2017

0 Comments

Impossible!

Section: Brain Teasers Category: Chess

Difficulty: Hard

Is it possible the following chess position to occur in a game?

SOLUTION

No, it is impossible. The White’s pawn from e2 should have captured the Black’s bishop from c8. In order for the bishop to get there, the pawn on c6 should have captured one of White’s rooks. It couldn’t be the rook from h1, so it should have been the rook from a1. But in order for the rook from a1 to get to c6, the pawns from b2 and c2 should have been moved to b3 and c4 respectively. However, in that case, the bishop from f1 couldn’t get to a4, since it has been blocked before the capture e2xf3.

Unknown Author November 19, 2017

0 Comments