Geometry 2 - Puzzle Prime

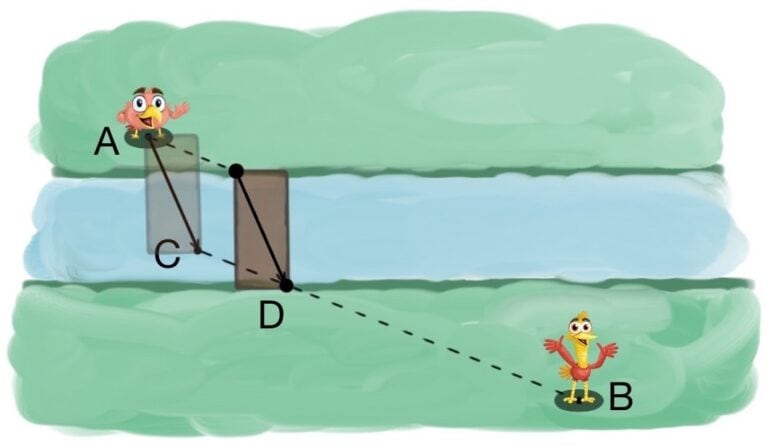
Bridge Over the River

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Geometry

Pinkbird is trying to get to Redbird across the river. Where should we place the bridge, so that the path between the two birds becomes as short as possible?

Remark: The bridge is exactly as long as the river is wide, and must be placed straight across it. Additionally, it has some positive width.

SOLUTION

Notice that no matter how the bridge gets placed over the river, the shortest path would be to go to its top left corner, then traverse it diagonally, then go from its bottom right corner to Redbird. The second part of the way has fixed length, so we must minimize the first part plus the third part. In order to do that, imagine we place the bridge, so that its top left corner is at the current position of Pinkbird – point A. If the bottom right corner ends up at point C, then we must connect C with the position of Redbird – point B, and wherever the line intersects the bottom shore – point D, that will be the best place for the bottom right corner of the bridge.

Unknown Author September 19, 2019

0 Comments

Every Acute Triangle

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Geometry

Consider an arbitrary acute triangle ABC. Let E be the intersection of the bisector at vertex C and the bisection of the side AB. Let F and G be the projections of E on AC and BC respectively.

Since E belongs to the bisection of AB, we must have AE = BE. Also, since E belongs to the bisector of C, we must have EF = EG. However, this would imply that triangles AEF and BGF are identical, and then AF = BF. We also have that CF = CG, which implies that AC = BC. The arbitrarily chosen triangle ABC is isosceles!

Can you find where the logic fails?

SOLUTION

The bisector of C and the bisection of AB always intersect outside the triangle, on the circumcircle. One of the points F and G always lies on the segment AC or BC, and the other one does not.

Unknown Author August 19, 2018

0 Comments

Obtuse Angle

Section: Brain Teasers Category: Mathematics

Difficulty: Expert Tags: Geometry

Prove that among any 9 points in (3D) space, there are three which form an obtuse angle.

SOLUTION

Let the points be labeled A₁, A₂, … , A₉, and P be their convex hull. If we assume that all angles among the points are not obtuse, then the interiors of the bodies P + A₁, P + A₂, … , P + A₉ should be all disjoint. That is because, for every A_i and A_j, P must be bound between the planes passing through A_i and A_j which are orthogonal to the segment A_iA_j. However, all of these 9 bodies have the same volume and are contained in the body P + P, which has 8 times larger volume. This is a contradiction, and therefore our assumption is wrong.

Puzzle Prime December 25, 2017

0 Comments

NASA and the Meteor

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced Tags: Geometry

NASA locates a meteor in outer space and concludes that it has either a cubical or spherical shape. In order to determine the exact shape, NASA lands a spacecraft on the meteor and lets a rover travel from the spacecraft to the opposite point on the planet. By measuring the relative position of the rover with respect to the spacecraft throughout its travel on the planet (in 3D coordinates), can NASA always determine the shape, no matter the route taken by the rover?

SOLUTION

The answer is NO.

The question is equivalent to analyzing the intersection of a cube and a sphere which share a common center. Thus the question gets reduced to figuring out whether such intersection, which is a curve, can connect two opposite points on the sphere/cube.

Let the edge of the cube has length 1. If you pick the radius of the sphere equal to √2/2, the intersection will consist of 6 circles inscribed in the sides of the cube. Then the rover can just move along these circles from one point to its opposite and NASA won’t be able to figure out the exact shape.

Remark: It is not hard to see that 2:√2 is the only edge-radius ratio, for which NASA can’t figure out the shape.

Unknown Author October 10, 2017

2 Comments