2 Matchsticks, 4 Squares
Move only 2 matchsticks so that you get 4 (identical) squares. There should not be any spare matchsticks left.
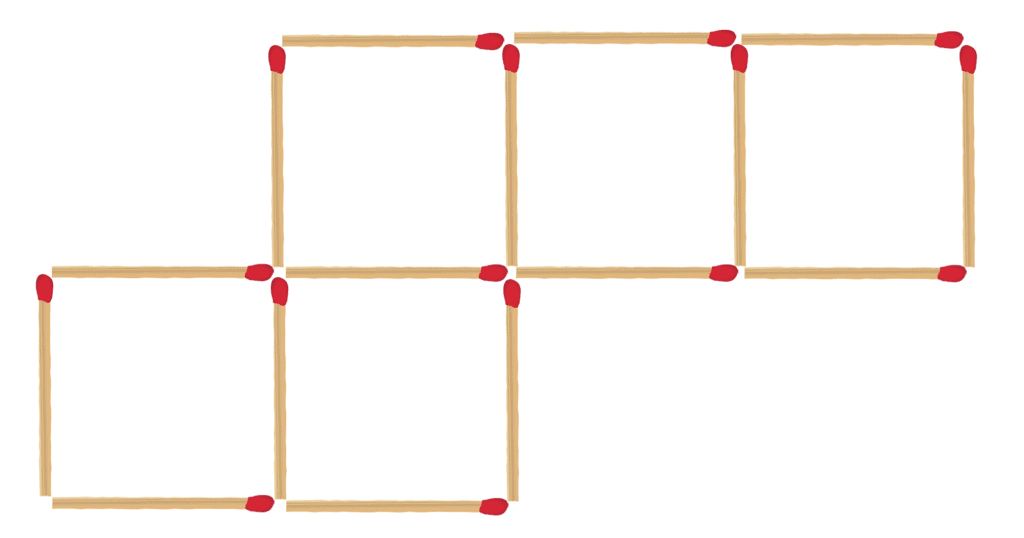
The solution is shown below.
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
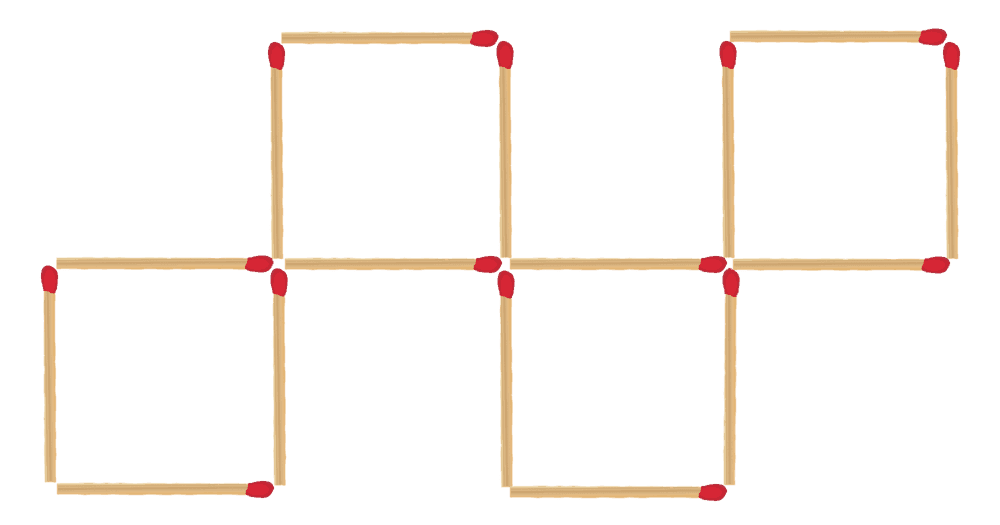
Move only 2 matchsticks so that you get 4 (identical) squares. There should not be any spare matchsticks left.

The solution is shown below.

One programmer draws on a sheet of paper several circles in a line, representing coins, and puts his thumb on the first circle, covering the rest with his hand. Then he asks another programmer to guess how many different head-tail combinations are possible if someone flips all the (imaginary) coins on the paper. The second programmer, without knowing the number of circles, takes the pen and writes down a number. Then the first programmer lifts his hand and sees that the correct answer is written on the paper. How did the second programmer manage to do this?

The second programmer wrote down “1” in front of the first circle. When the second programmer lifted his hand, he saw the number “10…00”, which is exactly the number of possible head-tail combinations in binary system.
What is the smallest number of moves needed to result in this unusual position?

The shortest game takes just 4 moves:
1. Nf3 e5
2. Nxe5 Ne7
3. Nxd7 Nec6
4. Nxb8 Nxb8
Take a small piece of paper – 4in by 6in, and scissors. Can you cut the paper in such a way, so that you can pass through it
Yes, you can, as shown on the image below.
Which is the best move for White in this position?

The best move is 1. Rc8+. Then either 1. … Kxb7 2. Rxd8, or 1. … Rxc8 2. Qxa7 Kxa7 3. bxc8 = N+, and Black loses both the Rook and the Queen.
A sundial has the fewest moving parts of any timepiece. Which has the most?
The hourglass, it has thousands of grains of sand.
You have 10 strings of pasta left on your plate. You randomly start tying up their ends, until there are no loose ends anymore. What is the average number of loops which are created?

The expected (average) number of loops at the end of the procedure is equal to the expected number of loops created after the first tying, plus the expected number of loops created after the second tying, etc. After each tying, the number of non-loop strings decreases by 1, and then the probabilities to create a new loop are 1/19, 1/17, 1/15, etc. Therefore, the answer is the sum 1/19 + 1/17 + 1/15 + … + 1/3 + 1/1 ~ 2.1.
What four-letter word can be written forward, backward or upside down, and can still be read from left to right?
The word NOON.
Imagine you have three identical bricks and want to find the common length of their main diagonals. What is the easiest way to do this using just a measuring tape?

PLace the bricks as shown on the image below, then measure the marked segment.

Get a bagel and a knife, then cut the bagel in two pieces which end up linked to each other.

The solution is presented HERE.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.