Square Triangle Circle
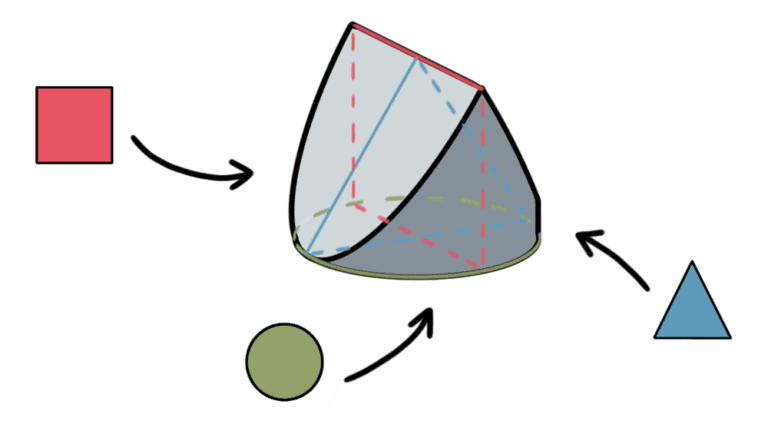
Can you draw a 3-dimensional object which looks like a square when looked from one side, a triangle when looked from a second side, and a circle when looked from a third side?

The object bellow satisfies the requirements.
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Can you draw a 3-dimensional object which looks like a square when looked from one side, a triangle when looked from a second side, and a circle when looked from a third side?

The object bellow satisfies the requirements.

Monday, six friends went camping. Tuesday, John, Jack, and James cooked some mushrooms. Wednesday came and they ate the mushrooms. Thursday found them dead. Exactly one friend survived, how come?
The six friends are called John, Jack, James, Tuesday, Wednesday, and Thursday. John, Jack, James, and Tuesday cooked the mushrooms. Wednesday joined them and they ate the mushrooms. Thursday was the one to find them dead, so he is the survivor.
Move just two matchsticks so that you get as large a number as possible.

You can take the two horizontal matchsticks from the first 0, form the number 11 with them to get 1100011. You can also make 1111000 if you don’t mind that the power’s font is larger than the base’s font, or use the quite uncommon operation “tetration” to get 1111000.
You are shown two cylinders – one of them is made of gold and hollow, the other one is made of alloy and solid. Both of them have the same weight, shape, and are colored in black. How can you figure out which cylinder is the golden one, without scratching the paint?
Simply roll the two cylinders on the ground. The hollow one will roll farther than the solid one
A dog is standing with three of its legs on a measuring scale, keeping its fourth leg in the air. If the scale is displaying 30lbs, how much will it display if the dog places its fourth leg on the scale?
The answer is 30lbs
If you hang a painting over two nails on the wall and remove one of the nails, the string of the painting will stay over the other nail, and the painting will keep hanging. Can you wrap a string around the nails in such a way, so that after removing any of the nails, the painting will fall?

The solution is shown below.

There are a fly and three spiders on the edges of a cube. If the spiders’ velocities are at least 1/3 of the fly’s velocity, and all insects can travel only along the edges of the cube, show that the spiders can eventually catch the fly.
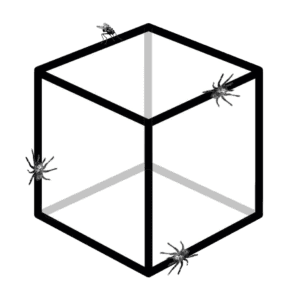
Choose two opposite edges of the cube, then let two of the spiders “protect” them from the fly. You can do this by keeping the distance from the two spiders to the edges’ endpoints at most 1/3 of the distance from the fly to these endpoints. The remaining parts of the cube do not contain any loops, so the third spider can easily catch the fly there.
There are only two barbers in one town. One of the barbers has a neat haircut and a clean working place. The other barber’s haircut is a total mess and his working place is dirty. Which barber would you choose to give you a haircut and why?
You should choose the second barber. Since there are only two barbers, the chances are that they give each other haircuts. Also, probably the second barber’s salon is dirtier because he has lots of work and does not have time to clean up properly.
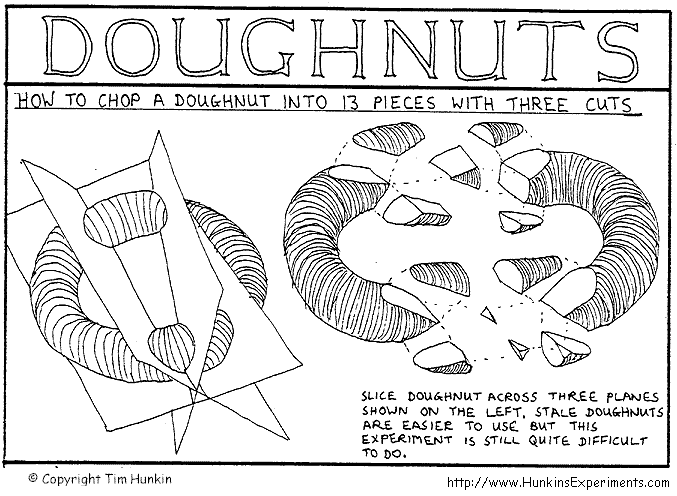
What is the largest number of pieces you can slice a doughnut into using only 3 cuts? You are not allowed to rearrange the pieces between the cuts.

You can get 13 pieces, as shown on the picture below.
There are 25 horses and you want to find the fastest 3 among them. You can race any 5 of the horses against each other and see the final standing, but not the running times. If all the horses have constant, permanent speeds, how many races do you need to organize in order to find the fastest 3?

Let us label the horses H1, H2, H3, H4, …, H24, H25.
We race H1 – H5 and (without loss of generality) find that H1 > H2 > H3 > H4 > H5. We conclude that H4, H5
We race H6 – H10 and (without loss of generality) find that H6 > H7 > H8 > H9 > H10. We conclude that H9, H10 are not among the fastest 3.
We race H11 – H15 and (without loss of generality) find that H11 > H12 > H13 > H14 > H15. We conclude that H14, H15 are not among the fastest 3.
We race H16 – H20 and (without loss of generality) find that H16 > H17 > H18 > H19 > H20. We conclude that H19, H20 are not among the fastest 3.
We race H21 – H25 and (without loss of generality) find that H21 > H22 > H23 > H24 > H25. We conclude that H24, H25 are not among the fastest 3.
We race H1, H6, H11, H16, H21 and (without loss of generality) find that H1 > H6 > H11 > H16 > H21. We conclude that H16, H21 are not among the fastest 3.
Now we know that H1 is the fastest horse and only H2, H3, H6, H7, H11 could complete the fastest three. We race them against each other and find which are the fastest two among them. We complete the task with only 7 races in total.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.