Mystery Mate
White plays and mates Black in one move. However, there is a mystery in this position that has to be revealed first.
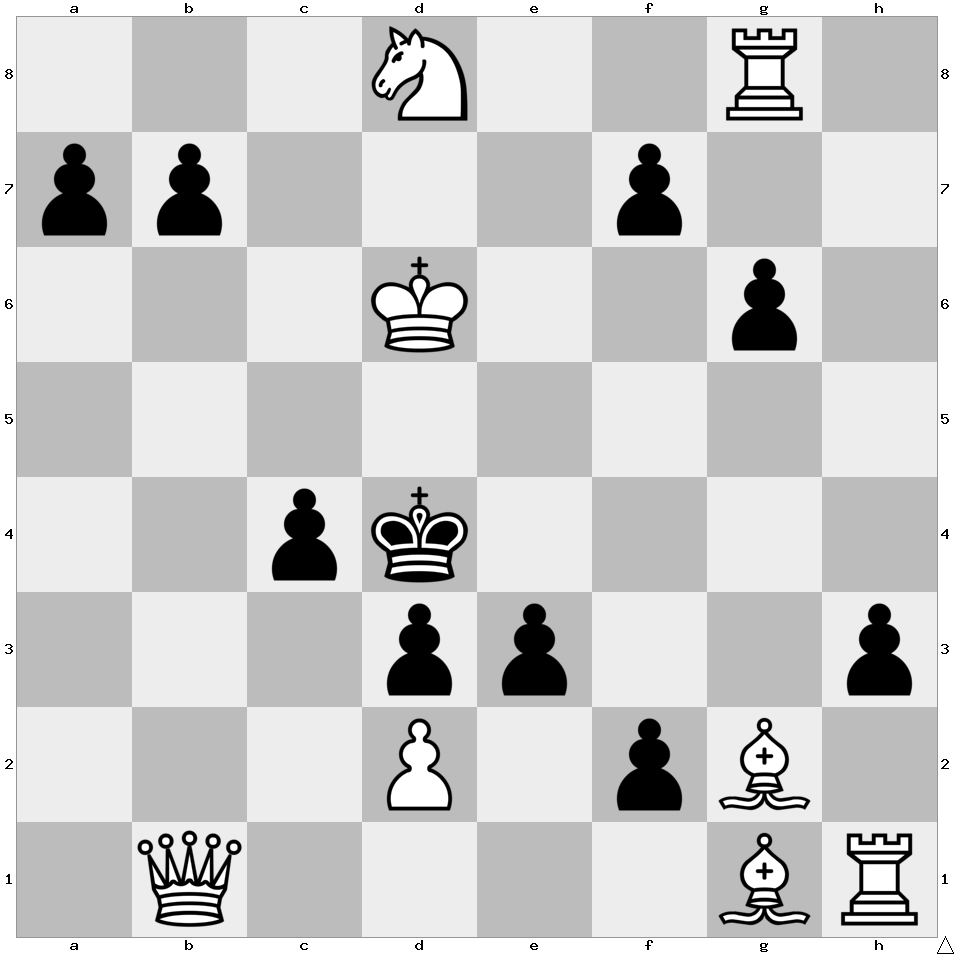
We do not know where this puzzle originated from. If you have any information, please let us know via email.
White plays and mates Black in one move. However, there is a mystery in this position that has to be revealed first.

Find a move for White, which does not result in a mate.

White to move and mate in 1.
Remark: There is only one correct answer.

The white king has made himself invisible. Where is he?
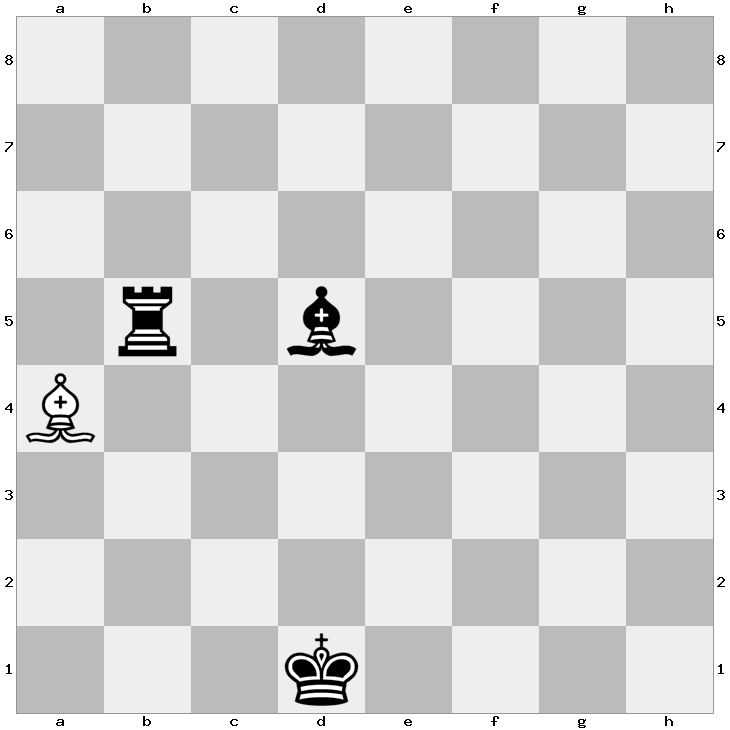
Design a game that takes less than 35 moves to get to the position below.

White starts and mates in 2 moves.

What was the last move made in this game?

If Black just made a move in this game, what is the minimum amount of moves that have been played?
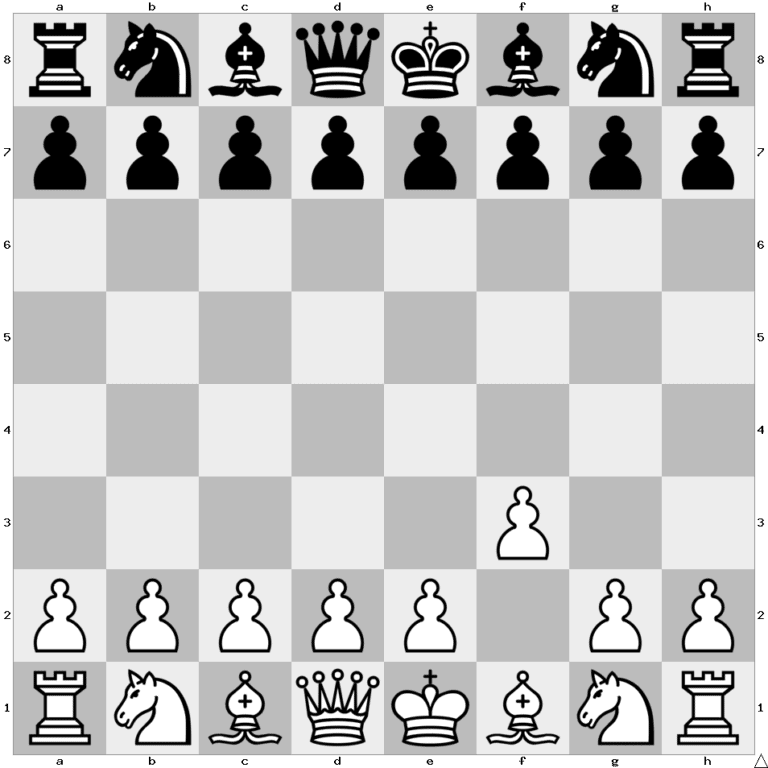
White to play and mate in 17 moves.

White to move and mate Black.

Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.
Notifications