Selfmate
White starts and forces Black to mate him in 8 moves.
SOLUTION
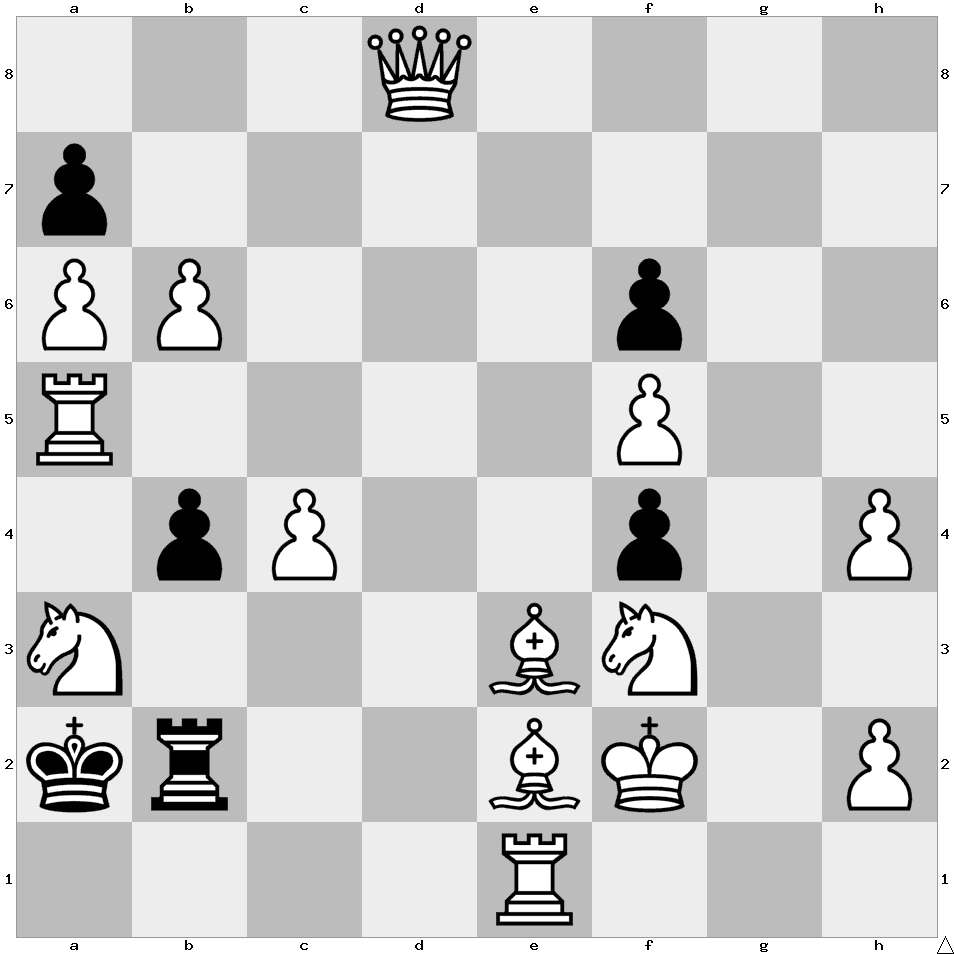
1. Nb1+ Kb3
2. Qd1+ Rc23
3. Bc1 axb6
4. Ra1 b5
5. Rh1 bxc4
6. Ke1 c3
7. Ng1 f3
8. Bf1 f2#
Category: Brain Teasers
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
WWII Planes
During World War II, the mathematician Abraham Wald was asked to help with determining which parts of the allied forces’ planes must be armored better. After examining the surviving American planes, he noticed that there were many holes in the fuselage, and very few in the engines. After careful thinking, he suggested that the armor on the engines must be improved. Why?
SOLUTION
Abraham Wald realized that the holes should have been distributed more evenly across the planes. Therefore the planes which had more holes in the fuselage survived, while the planes which had more holes in the engines got destroyed.
Roll a Pencil
You roll a 5 sided pencil on the table. On one of its sides, it is written “HB Pencil”, the others are blank. What is the chance that the side with text on it ends up straight on top?
SOLUTION
The chance is 0%. Since the pencil has an odd number of sides, it is impossible that any of them ends up straight on top.
Truck Too Tall
A driver needs to pass under a bridge, but his truck is one inch too tall. However, despite this issue, the driver finds a way to continue further. How?
SOLUTION
He deflated slightly the tires of the truck.
Cut the Paper
You have a sheet of paper and a rectangular piece cut from it, as shown in the picture. What is the easiest way to cut the paper into two pieces with
SOLUTION
Make a cut through the centers of the small and the big rectangle. The cut will split both the area of the big and the small (absent) rectangle by half, and therefore will do the same to their difference – the given sheet of paper.
Securing the Box
There are 5 people who possess a box. You are allowed to secure the box with as many different locks as you like and distribute any combination of keys for these locks to any people among the 5. Find the least number of locks needed, so that no 2 people can open the box, but any cannot people can open it.
SOLUTION
For every subset of 2 people you pick among the 5, there should be a lock which none of the 2 can unlock, and each of the remaining 3 people can unlock. Clearly, the lock in question cannot be the same for any two different subsets of 2 people you choose. Therefore the number of locks you need is at least the number of different 2-element subsets of a 5-element set, which is 5!/(2!3!)=10. This number is sufficient as well – just give keys to a different group of 3 people for every lock.
Relabeling Dices
Can you relabel two 6-sided dices, so that every face has
SOLUTION
Yes, you can do this. The easiest way is to use generating functions. Using simple polynomial algebra, you can see that
(x + x2 + x3 + x4 + x5 + x6)2 = (x + 2x2 + 2x3 + x4)(x + x3 + x4 + x5 + x6 + x8).
Therefore, if you take a dice with spots {1, 2, 2, 3, 3, 4}, and a dice with spots {1, 3, 4, 5, 6, 8}, their sum will have the same probability distribution.
The Lion and the Zebras
The lion plays a deadly game against a group of 100 zebras that takes place in the steppe (an infinite plane). The lion starts in the origin with coordinates (0,0), while the 100 zebras may arbitrarily pick their 100 starting positions. The lion and the group of zebras move alternately:
- In a lion move, the lion moves from its current position to a position at most 100 meters away.
- In a zebra move, one of the 100 zebras moves from its current position to a position at most 100 meters away.
- The lion wins the game as soon as he manages to catch one of the zebras.
Will the lion always win the game after a finite number of moves? Or is there a strategy for the zebras that lets them survive forever?
SOLUTION
The zebras can survive forever. They choose 100 parallel strips with width 300m each, then start on points on their mid-lines. If the lion lands on some zebra’s strip, the zebra simply jumps 100m away from the lion,
Source:
Trick Mules
In order to solve this puzzle, you must print the image below and cut it in 3 pieces along the dotted lines. The question is, can you after that rearrange these pieces
SOLUTION
The solution is shown below.
Rich and Poor
Who is richer – the richest among the poor or the poorest among the rich?
SOLUTION
The poorest among the rich is richer than the richest among the poor. That is because any rich person is by default richer than any poor person.