Her Name
Mary’s father has 4 children. Their names are April, May, June and ???
SOLUTION
Mary.
Category: Brain Teasers
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Obtuse Angle
Prove that among any 9 points in (3D) space, there are three which form an obtuse angle.
SOLUTION
Let the points be labeled A1, A2, … , A9, and P be their convex hull. If we assume that all angles among the points are not obtuse, then the interiors of the bodies P + A1, P + A2, … , P + A9 should be all disjoint. That is because, for every Ai and Aj, P must be bound between the planes passing through Ai and Aj which are orthogonal to the segment AiAj. However, all of these 9 bodies have the same volume and are contained in the body P + P, which has 8 times larger volume. This is a contradiction, and therefore our assumption is wrong.
Lost Boarding Pass
There are 100 passengers which are trying to get on a plane. The first passenger, however, has lost his boarding pass, so decides to sit on an arbitrary seat. Each successive passenger either sits on his own seat if it is empty or on an arbitrary other if it is taken. What is the chance that the last person will sit
SOLUTION
The chance is 50%. Indeed, the last passenger will either have to sit in his own seat or the one which belongs to the first passenger. Since there hasn’t
Mysterious Polynomial
You are given a polynomial P(x) of unknown degree with coefficients which are non-negative integers. You don’t know any of the coefficients, but you are allowed to evaluate the polynomial at any point you choose. What is the smallest number of evaluations you need to use, so that can find the degree and the coefficients of P(x)?
SOLUTION
Just 2 evaluations are enough. First, get P(1). This will give you an upper bound on the number of digits of the largest coefficient of the polynomial, let’s say that is N. Now evaluate the polynomial at the point M = 10 to the power of N. This will make all of the coefficients of P appear in the number P(M), separated by strings of zeros.
Broken Clock
An old wall clock falls on the ground and breaks into 3 pieces. Describe the pieces, if you know that the sum of the numbers on each of them is the same.
SOLUTION
The total of all numbers on the clock is 1 + 2 + … + 12 = 78. Therefore each piece must contain numbers with total sum 26. The only way for this to happen is if the pieces are broken via 3 parallel lines – {1, 2, 11, 12}, {3, 4, 9, 10}, {5, 6, 7, 8}.
Cover the Grid
You must cover a 7×7 grid with L-shaped triminos and S-shaped tetrominos, without overlapping (flipping and rotating is permitted). What is the minimum number of pieces you can use in order to do this?
Remark: All pieces must be placed entirely on the board.
SOLUTION
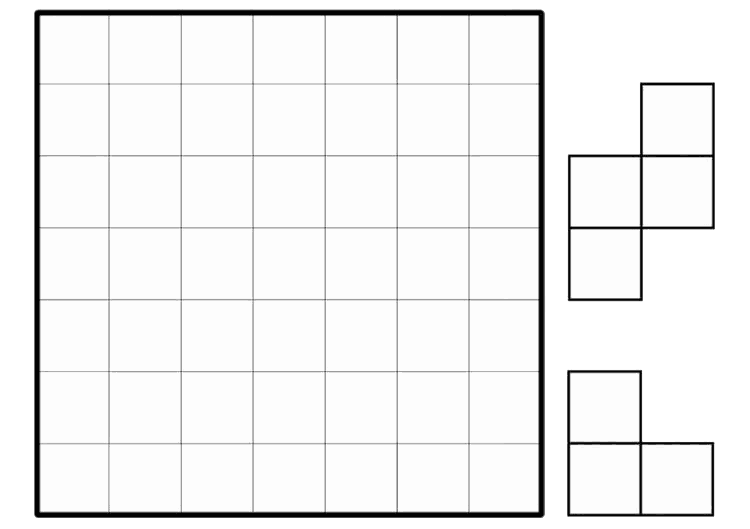
Consider all cells in the grid which lie in an odd row and odd column – there are 16 of them. Since each of the two pieces can cover at most 1 of these cells, we need at least 16 pieces. Giving an example with 16 pieces is easy.
Legs of a Horse
One horse traveled for a whole day and at the end
SOLUTION
The horse was operating a mill and was traveling in a circle. Thus its outer legs covered larger distance than its inner legs.
10 Prisoners, 10 Keys, 2 Weeks
One day, the warden of a prison is, like most wardens in puzzles, feeling a little capricious and decides that he wants to get rid of his prisoners, one way or another. He gathers all the prisoners in the yard and explains to them – “Tonight, I will go to each of you, hand you a key, and tell you who has your key. Each day after that, while the others are out of the cells and no one is watching, I will allow each of you to place your key in someone else’s cell – and each night, you may collect the keys in your own cell. If at any point, you are certain that everyone has the key to their own cell, you may summon me, at which point each of you will open your own cell and walk free. If anyone has the wrong key, everyone will be executed then and there. You may discuss your strategy before tonight, but afterward
That night, just as promised, the warden went to each cell and gave each prisoner a key. As he handed each prisoner the key, he whispered to them the name of the person possessing the key to their cell. The keys were entirely indistinguishable from one another, but that was okay, because the prisoners had not counted on being able to tell anything about them. Indeed, the prisoners all seemed confident.
What was their strategy? How could they beat the warden’s game?
SOLUTION
We assume the cells in the prison are arranged in a circle. The prisoners agree every day each of them to pass the key they receive to their left neighbor, except for their own key which they keep. It is easy to figure out which key is their own since they can easily calculate when they will receive it. For example, if prisoner 8 knows that his key is at prisoner 3 in the beginning, then he will get it on the 5th day. Therefore, within 10 days, all prisoners will have their own keys.
Source:
Half Move Mate
White plays and mates in half a move. How is it possible?
SOLUTION
White completes his castle by putting the rook on f1 and mating Black.
Impossible!
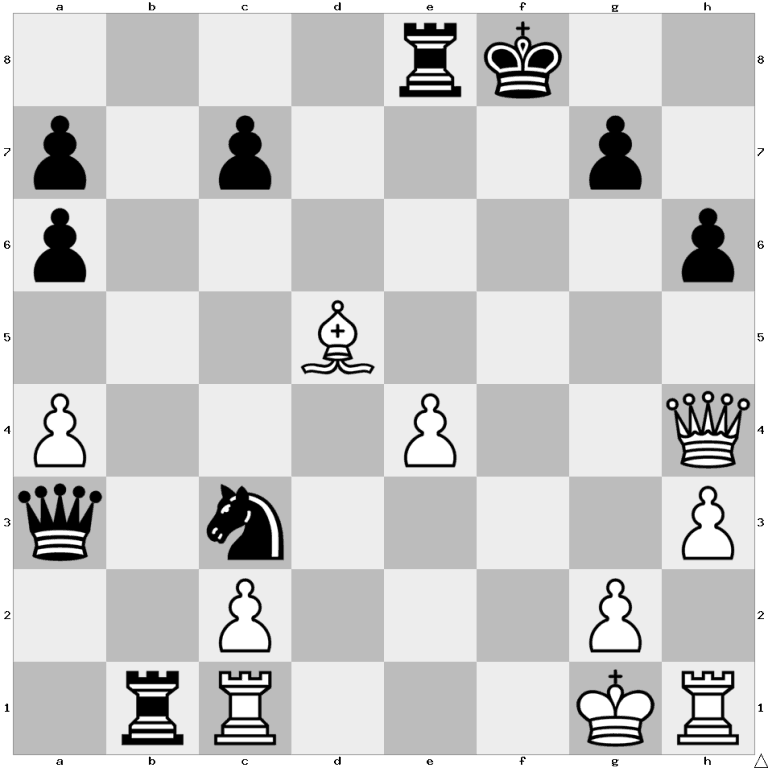
Is it possible the following chess position to occur in a game?
SOLUTION
No, it is impossible. The White’s pawn from e2 should have captured the Black’s bishop from c8. In order for the bishop to get there, the pawn on c6 should have captured one of White’s rooks. It couldn’t be the rook from h1, so it should have been the rook from a1. But in order for the rook from a1 to get to c6, the pawns from b2 and c2 should have been moved to b3 and c4 respectively. However, in that case