The Gingerbread Dog
Can you cut Sam Loyd’s gingerbread dog into two identical pieces?
SOLUTION
The solution is shown below.
Category: Brain Teasers
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
Samuel Loyd (1841 – 1911), born in Philadelphia and raised in New York City, was an American chess player, chess composer, puzzle author, and recreational mathematician. As a chess composer, he authored a number of chess problems, often with interesting themes. At his peak, Loyd was one of the best chess players in the US and was ranked 15th in the world, according to chessmetrics.com.
Stopped Wall Clock
Ben has a wall clock in his room, but he didn’t wind it one day, so it stopped working. Later that day he left his house, walked to his best friend’s place, who has his own, always precise clock, stayed there for a while, then walked back home. When he arrived, he went to his wall clock and adjusted it to show the correct time. How did Ben do it, if he didn’t see any other clocks during the day, except for the one at his best friend’s place?
SOLUTION
Before Ben left his place, he winded his clock. When he went to his friend’s place, he noted for how long he stayed there, say X, and at what time he left, say Y. After Ben got back home, he looked at his own wall clock and calculated the time he was outside, say Z. Then he concluded that the time he was walking was Z – X in total, and therefore it took him (Z – X)/2 time to get from his friend’s place to his own house. He added Y (the time he left his friend’s place) and got Y + (Z – X)/2, the correct time.
Mate in 1
White to move and mate in 1.
Remark: There is only one correct answer.
SOLUTION
The answer is Qa3#.
FEATURED
Princess in a Palace
A princess is living in a palace which has 17 bedrooms, arranged in a line. There is a door between
SOLUTION
You knock on doors:
2, 3,…, 15, 16, 16, 15,…, 3, 2.
This adds up to a total of 30 days exactly. If during the first 15 days you don’t find the princess, this means that every time you were knocking on an even door, she was in an odd room, and vice versa. Now it is easy to see that in the next 15 days you can’t miss her.
Unfaithful
Jack is looking at Anne, but Anne is looking at George. Jack is married, but George is not. Is a married person looking at an unmarried person?
- Yes
- No
- Cannot be determined
SOLUTION
The answer is YES. If Anne is unmarried, then Jack is married and is looking at an unmarried person. If not, then she is married and is looking at an unmarried person.
Invisible King
The white king has made himself invisible. Where is he?
SOLUTION
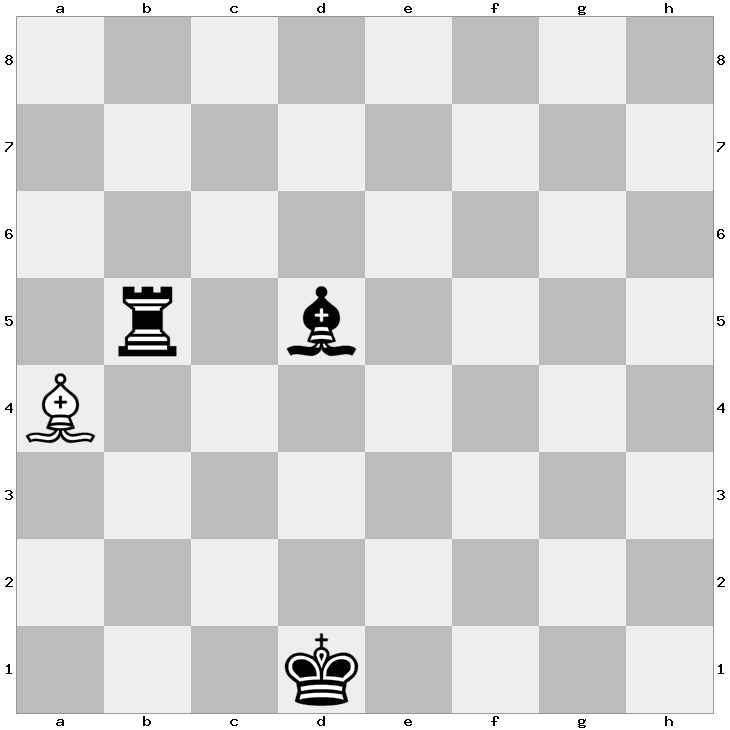
The white king is on c3. Since he cannot be currently on b3 (he will be in double check from the black rook and the black bishop), Black must be currently in check from the white bishop. That’s possible only if White has given a discovered check with his king. That’s possible only if on the previous move, the white king was on b3 and was in double check. The only possible way for this to happen is if Black gave two discovered checks at the same time. The one way to do this is if a black pawn on b4 captured a white pawn on c3 using en passant. Thus after b4xc3, the white king has just captured the black pawn on c3, and that is where he is currently hiding.
Product
What is the product (x – a)(x – b)…(x – z) equal to?
SOLUTION
This product is equal to (x – a)(x – b)…(x – x)(x – y)(x – z) = 0.
Move Move Chess
Consider a chess game in which every player is allowed to move twice per turn. Show that Black does not have a winning strategy.
SOLUTION
Assume Black has a winning strategy. Then if White plays Kb1-Kc3 and Kc3-b1 on his first turn, the game basically will start all over again, but with Black moving first. Therefore White will have a winning strategy, which is a contradiction.
Codex Enigmatum
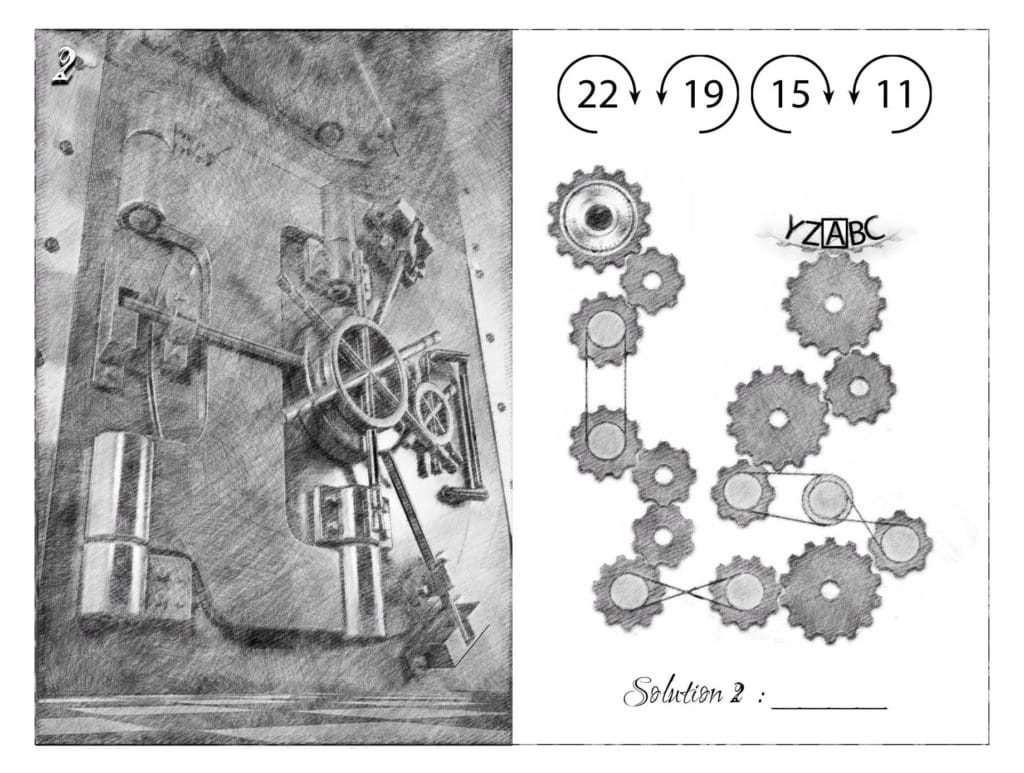
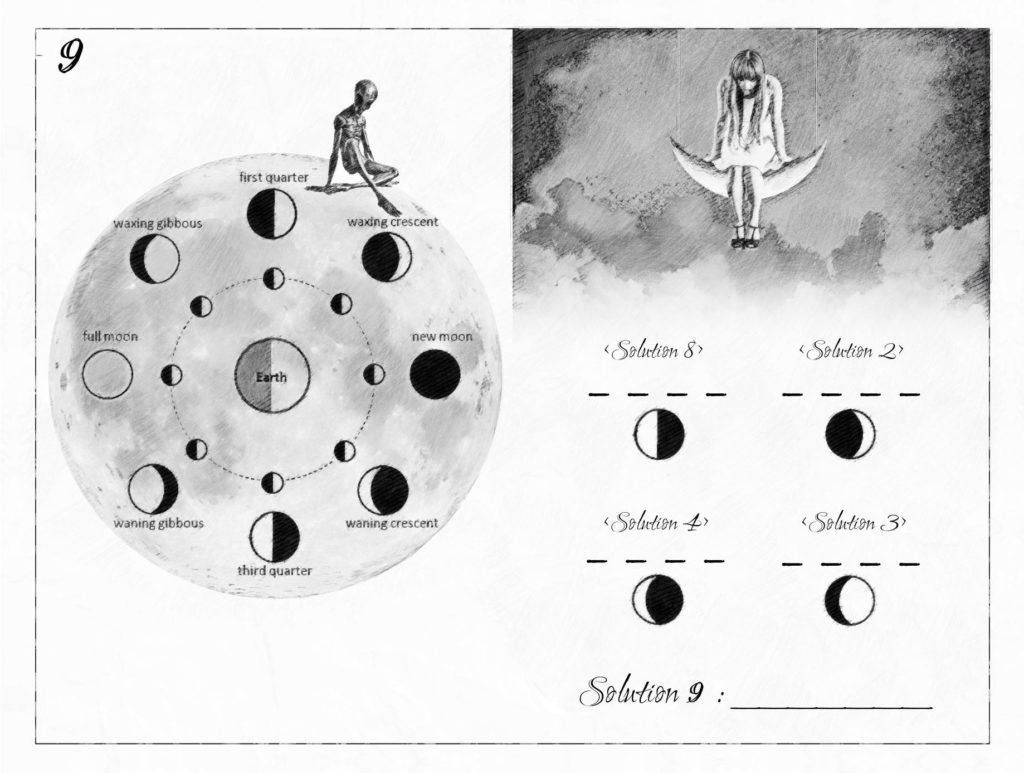
These are a few enigmas from the puzzle book CODEX ENIGMATUM. What is the answer to puzzle #9?
SOLUTION
- Puzzle #2 After turning the first wheel 22 times to the right, then 19 times to the left, then 15 times to the right, and finally 11 times to the left, the final wheel will spell the word EXIT.
- Puzzle #3 The total number of spots on the hidden sides of the die on the left is 6, which corresponds to the sixth letter in the alphabet – F. Therefore, the four dice on the right correspond to the letters K, I, N, G.
- Puzzle #4 In the mosaic on the right, you can find a little star which contains pieces with letters H, I, D, E.
- Puzzle #6 If you trace the signature on the paper, starting from the large C, you will pass through the letters C, O, N, T, I, N, U, O, U, S.
- Puzzle #8 The picture on the left and the answer to puzzle #6 (“continuous”) suggest that we have to consider the images on the right which can be drawn continuously, without taking off the pencil from the paper or passing through any segment twice. These images are labeled with the letters N, O, S, E.
- Puzzle #9 The first 2 letters from the word NOSE spell NO. The last letter from the word EXIT is T. The first letter from the word HIDE is H. The last three letters from the word KING spell ING. When you combine all of them, you get the word NOTHING.
Source:
Moms’ Talk
Two moms, Sarah and Courtney, are talking to each other.
Sarah: I have two children
What is the probability that both of Sarah’s children are boys?
Courtney: Me too! Do
What is the probability that both of Courtney’s children are boys?
Sarah: Yes, I do! What is your younger child?
What is the probability that both of Sarah’s children are boys?
Courtney: It is a boy. He is so mischievous!
What is the probability that both of Courtney’s children are boys?
Sarah: Is he Sagittarius? Sagittarius boys are known to drive their mothers crazy. I can testify from personal experience.
What is the probability that both of Sarah’s children are boys?
Courtney: No, but actually I have the opposite personal experience to yours.
What is the probability that both of Courtney’s children are boys?
Sarah: Well, I guess astrology does not always get it right.
Courtney: I assume it does about half of the time.
SOLUTION
The answers are: ~1/4, ~1/4, ~1/3, ~1/2, ~23/47, 1.
Explanation:
Initially, we do not have any information about the children and therefore the chance that both of them boys is 1/2 × 1/2. This applies to the first and the second question.
After Sarah says that she has at least one boy, there are equal possibilities that she has Boy + Boy, Boy + Girl, or Girl + Boy. Therefore, the chance that both children are boys is 1/3.
After Courtney says that her younger child is a boy, the only remaining question is what is the gender of her older child, and therefore the chance is 1/2.
The fifth exchange implies that Sarah has a Sagittarius boy. There are 23 combinations such that both children are boys and at least one of them is Sagittarius. There are 47 combinations such that at least one of the children is a Sagittarius boy. Therefore, the chance that both children are boys is 23/47.
Finally, Courtney says that her younger child, which is a boy, is not Sagittarius, but her personal experience with Sagittarius boys is positive. Therefore, her older child is a Sagittarius boy and the chance is 1.